Точка, линия, прямая, луч, отрезок, ломанная | Математика (геометрия)

Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различатьABC123Можно нарисовать на листке бумаги три точки “А” и предложить ребёнку провести линию через две точки “А”. Но как понять через какие? A A A
Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет
Обозначается строчными (маленькими) латинскими буквамиabc
Линия может быть
- замкнутой, если её начало и конец находятся в одной точке,
- разомкнутой, если её начало и конец не соединены
Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру. Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
- самопересекающейся
- без самопересечений
Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны
Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны
Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямойaBA
Прямые могут быть
- пересекающимися, если имеют общую точку. Две прямые могут пересекаться только в одной точке.
- перпендикулярными, если пересекаются под прямым углом (90°).
- параллельными, если не пересекаются, не имеют общей точки.
Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону
У луча света на картинке начальной точкой является солнце
Точка разделяет прямую на две части — два лучаA
Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на лучеaBA
Лучи совпадают, если
- расположены на одной и той же прямой,
- начинаются в одной точке,
- направлены в одну сторону
CBA
Отрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину. Длина отрезка — это расстояние между его начальной и конечной точками
Через одну точку можно провести любое число линий, в том числе прямых
Через две точки — неограниченное количество кривых, но только одну прямуюBABA
От прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками.
Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезокBAЗадача: где прямая, луч, отрезок, кривая?
Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°
Длинный отрезок «поломали» на несколько коротких
Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.
Обозначается ломанная перечислением всех её вершин.ABCDE646212752
Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305Задача: какая ломанная длиннее, а у какой больше вершин? У первой линии все звенья одинаковой длины, а именно по 13см. У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
Многоугольник — это замкнутая ломанная линия
Стороны многоугольника (помогут запомнить выражения: “пойти на все четыре стороны”, “бежать в сторону дома”, “с какой стороны стола сядешь?”) — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.
Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
Обозначается многоугольник перечислением всех его вершин.ABCDEF120605812298141
Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599
Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т.д.
Источник: http://shpargalkablog.ru/2015/11/point-line-straight-ray-segment.html
Прямая луч отрезок правило
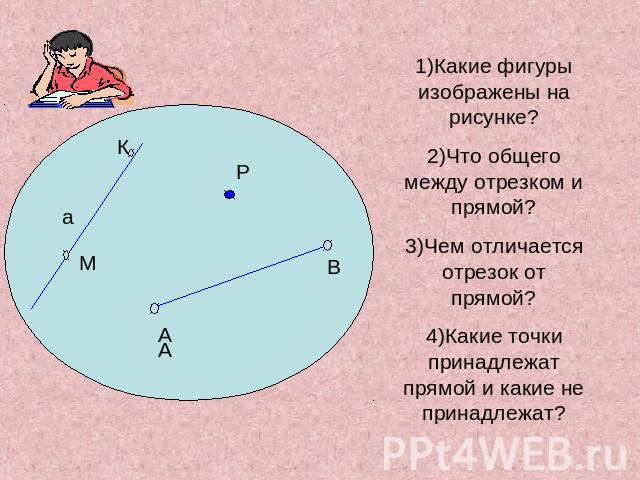
Точка О разбивает прямую AB на две части. Что напоминает каждая из частей? Чем каждая часть отличается от прямой и отрезка?
Отметь цветным карандашом начало каждого луча. Как обозначен первый луч? Можно ли поменять местами буквы? Почему? Обозначь остальные лучи.
Решение
Обведи с помощью линейки на чертеже прямые линии красным карандашом, лучи — синим, а отрезки — зелёным:
- «Машенька испекла вчера 32 пирожка, а сегодня — на 4 пирожка больше».Какие вопросы можно поставить к этому условию, чтобы получилась задача:
- 1) Сколько пирожков испекла Машенька вчера?
- 2) Сколько пирожков испекла она сегодня?
- 3) С какой начинкой были пирожки?
- 4) Сколько пирожков испекла Машенька за 2 дня?
- Подбери к полученным задачам подходящие схемы и реши их:
- а) Заменить букву о на букву и. Заменить букву и на букву о.
- б) 1м 5см выразить в сантиметрах. 105см выразить в метрах и сантиметрах.
- 1) 56 + 8 = 64
- 2) 64 + 56 = 120
- 3) 180 — 120 = 60
- 60кг продали в 3 день.
- замкнутой , если её начало и конец находятся в одной точке,
- разомкнутой , если её начало и конец не соединены
- самопересекающейся
- без самопересечений
- пересекающимися , если имеют общую точку. Две прямые могут пересекаться только в одной точке.
- перпендикулярными , если пересекаются под прямым углом (90°).
- параллельными , если не пересекаются, не имеют общей точки.
- расположены на одной и той же прямой,
- начинаются в одной точке,
- направлены в одну сторону
-
Через две точки — неограниченное количество кривых, но только одну прямую
кривые линии, проходящие через две точки
прямая линия AB
От прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками.
- ✂ B A ✂
В одном вагоне поезда едут 46 человек, а в другом — на 18 человек меньше. Сколько человек едут в двух вагонах?
- Что надо поставить вместо знака вопроса? Назови взаимно обратные операции.
Реши задачу, а затем составь и реши обратную задачу:«В ларёк привезли 180 кг винограда и продали его за 3 дня. В первый день продали 56 кг, а во второй — на 8 кг больше. Сколько килограммов винограда продали в третий день?»
Найди закономерность и вставь пропущенные числа. Кто быстрее назовёт все числа этого ряда?mat-zadachi.ru
Точка, линия, прямая, луч, отрезок, ломанная | Математика (геометрия)
Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение
Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать
точка A, точка B, точка C
точка 1, точка 2, точка 3
Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет
Обозначается строчными (маленькими) латинскими буквами
линия a, линия b, линия c
Линия может быть
Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороныОбозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
прямая линия a
Прямые могут быть
У луча света на картинке начальной точкой является солнце
Точка разделяет прямую на две части — два луча A A
Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче
Лучи совпадают, если
Через одну точку можно провести любое число линий, в том числе прямых
Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок
отрезок AB
Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°
Длинный отрезок «поломали» на несколько коротких
Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.
Обозначается ломанная перечислением всех её вершин.
ломанная линия ABCDE
вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E
звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE
звено AB и звено BC являются смежными
звено BC и звено CD являются смежными
звено CD и звено DE являются смежными
Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305
Многоугольник — это замкнутая ломанная линия
Стороны многоугольника (помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.
Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
Обозначается многоугольник перечислением всех его вершин.
замкнутая ломанная линия, не имеющая самопересечения, ABCDEF
многоугольник ABCDEF
вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F
вершина A и вершина B являются соседними
вершина B и вершина C являются соседними
вершина C и вершина D являются соседними
вершина D и вершина E являются соседними
вершина E и вершина F являются соседними
вершина F и вершина A являются соседними
сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF
сторона AB и сторона BC являются смежными
сторона BC и сторона CD являются смежными
сторона CD и сторона DE являются смежными
сторона DE и сторона EF являются смежными
сторона EF и сторона FA являются смежными
A B C D E F 120 60 58 122 98 141
Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599
Многоугольник с тремя вершинами называется треугольником , с четырьмя — четырёхугольником , с пятью — пятиугольником и т.д.
shpargalkablog.ru
Основы геометрии
Геометрия — это раздел математики, изучающий геометрические фигуры и их свойства.
Познакомимся с основными геометрическими понятиями, изучаемыми в начальной школе.
Точка — это основная и самая простая геометрическая фигура.
В геометрии точка обозначается заглавной латинской буквой или цифрой. Многие латинские буквы по написанию похожи на английские буквы.
В тексте точку обозначают следующим символом: « (·) A » — точка « А ».
Прямая — это самая простая геометрическая фигура, которая не имеет ни начала, ни конца.
Слова «не имеет ни начала, ни конца» говорят о том, что прямая бесконечна.
Способы обозначения прямых
Двумя заглавными латинскими буквами в том случае, если этими буквами обозначены точки, расположенные на прямой.
Луч — это часть прямой линии, которая расположена по одну сторону от какой-либо точки. У луча есть начало , но нет конца .
Способы обозначения лучей
Двумя заглавными латинскими буквами в том случае, когда первая точка — начало луча, а вторая точка лежит на луче.
https://www.youtube.com/watch?v=9kYdHU47qdY
Отрезок — это часть прямой линии, которая ограничена двумя точками (концами отрезка). У отрезка есть и начало , и конец .
Основное свойство отрезка — это его длина.
Длина отрезка — это расстояние между его концами.
В математике отрезок обозначается заглавными латинскими буквами.
Ломаная — это геометрическая фигура, состоящая из точек, которые соединены отрезками.
Вершины ломаной — это точки, в которых соединяются отрезки, образующие ломаную.
Звенья ломаной — это отрезки ломаной.
В математике ломаная обозначается заглавными латинскими буквами.
Ломаная « ABCD ».Вершины ломаной — A, B, C, D .
Звенья ломаной — AB, BC, CD.
Чтобы найти длину ломаной, необходимо сложить длины всех её звеньев (отрезков), из которых она состоит.
KLCM = KL + LC + CM = 3 см + 2 см + 2 см = 7 см
Вот мы и познакомились с основами геометрии. Теперь мы готовы рассмотреть не менее важную геометрическую фигуру — угол. Для этого перейдите на следующую страницу, нажав на кнопку «Посмотреть содержание темы» вверху страницы.
math-prosto.ru
Точка. Отрезок. Луч. Прямая. Числовая прямая
Мы рассмотрим каждую из тем, а в конце будут даны тесты по темам.
Точка в математике
Что такое точка в математике? Математическая точка не имеет размеров и обозначается заглавными латинскими буквами: A, B, C, D, F и т.д.
На рисунке можно видеть изображение точек A, B, C, D, F, E, M, T, S.
Отрезок в математике
Что такое отрезок в математике? На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы. Отрезок в математике — это совокупность всех точек, лежащих на прямой между концами отрезка. Концы отрезка — две граничные точки.
На рисунке мы видим следующее: отрезки [A;C],[C;D],[D;M],[M;F],[F;E] и [E;T], а также две точки B и S.
Прямая в математике
Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности. Прямая в математике обозначается двумя любыми точками прямой. Для объяснения понятия прямой ученику можно сказать, что прямая — это отрезок, который не имеет двух концов.
На рисунке изображены две прямые: CD и EF.
Луч в математике
Что же такое луч? Определение луча в математике: луч — часть прямой, которая имеет начало и не имеет конца. В названии луча присутствуют две буквы, например, DC. Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
На рисунке изображены лучи: DC, KC, EF, MT, MS. Лучи KC и KD — один луч, т.к. у них общее начало.
Числовая прямая в математике
Определение числовой прямой в математике: прямая, точки которой отмечают числа, называют числовой прямой.
На рисунке изображена числовая прямая, а также луч OD и ED
www.nado5.ru
Основные геометрические фигуры
К основным геометрическим фигурам на плоскости относятся точка и прямая линия. Отрезок, луч, ломаная линия — простейшие геометрические фигуры на плоскости.
Точка — это самая малая геометрическая фигура, которая является основой всех прочих построений (фигур) в любом изображении или чертеже.
Всякая более сложная геометрическая фигура — это множество точек, которые обладают определенным свойством, характерным только для этой фигуры.
Прямую линию , или прямую, можно представить себе как бесчисленное множество точек, которые расположены на одной линии, не имеющей ни начала, ни конца. На листе бумаги мы видим только часть прямой линии, так как она бесконечна. Прямая изображается так:
Часть прямой линии, ограниченная с двух сторон точками, называется отрезком прямой, или отрезком . Отрезок изображается так:
Луч — это направленная полупрямая, которая имеет точку начала и не имеет конца. Луч изображается так:
Если на прямой вы поставили точку, то этой точкой прямая разбивается па два луча, противоположно направленных. Такие лучи называются дополнительными.
Ломаная линия — это несколько отрезков, соединенных между собой так, что конец первого отрезка является началом второго отрезка, а конец второго отрезка — началом третьего отрезка и т. д., при этом соседние (имеющие одну общую точку) отрезки расположены не на одной прямой. Если конец последнего отрезка не совпадает с началом первого, то такая ломаная линия называется незамкнутой.
Выше изображена трехзвенная ломаная линия.
Если конец последнего отрезка ломаной совпадает с началом первого отрезка, то такая ломаная линия называется замкнутой. Примером замкнутой ломаной служит любой многоугольник:
Четырехзвенная замкнутая ломаная линия — четырехугольник
Трехзвенная замкнутая ломаная линия — треугольник
Плоскость , как и прямая, — это первичное понятие, не имеющее определения. У плоскости, как и у прямой, нельзя видеть ни начала, ни конца. Мы рассматриваем только часть плоскости, которая ограничена замкнутой ломаной линией.
Примером плоскости является поверхность вашего рабочего стола, тетрадный лист, любая гладкая поверхность. Плоскость можно изобразить как заштрихованную
геометрическую фигуру:
shkolo.ru
Источник: http://mpo-kamena.ru/prjamaja-luch-otrezok-pravilo-/8881/
Тема: Прямая. Луч. Отрезок

Разработка урока математики во 2 классе
…»
Цели:
1. Закрепить представления о понятиях «прямая», «луч», «отрезок». Учить детей распознавать прямые, лучи, отрезки; изображать их с помощью линейки; находить и обозначать точки их пересечения.
2. Повторить изученное; закреплять навыки сложения и вычитания трёхзначных чисел.
3.Развивать творческое мышление, интерес к математике.
I. Оргмомент.
II. Актуализация знаний.
1 Индивидуальная работа.
- Расшифруй слово, расположив результаты действий в порядке возрастания.
О 31-9 Ч 18+17 А 87+13
Т 24-7 К 60-12
17 22 35 48 100
Т О Ч К А
2 Фронтальная работа.
- Если правильно выполните все задания, то сможете прочитать название страны, куда мы отправимся во время изучения новой темы.
а) Продолжи ряд чисел 3, 6, 9….(мет) (Слайд 1,2)
б) Как удобнее вычислить? 13+16+19+22+25+28+31+34+37 (о) (Слайд 3,4)
в) Какие цифры пропущены? (Слайд 5,6)
4
6
8
5
6
5
(ге)
г) Сколько треугольников на рисунке? (рия)
(Слайд 7,8)
III. Работа над темой.
Сказка про Точку.
Сегодня мы отправимся в увлекательное путешествие по стране Геометрия. Встречает нас здесь королева этой страны, без которой нельзя построить ни одну фигуру. Кто она? (Точка)
Жила была Точка. Она была очень любопытна и хотела всё знать. Увидит незнакомую линию и непременно спросит:
- Как эта линия называется? Длинная она или короткая?
Подумала однажды Точка: «Как же я смогу все узнать, если всегда буду жить на одном месте? Отправлюсь-ка я путешествовать!»
Ребята, вы готовы совершить путешествие вместе с Точкой? (Да)
Сказано — сделано. Вышла Точка на прямую линию и пошла по этой линии. ( Слайд 10)
Шла, шла по прямой линии. Долго шла.Устала. Остановилась и говорит: « Долго ли я ещё буду идти?»
–Ребята, скоро ли конец прямой линии?(У прямой нет конца)
–Тогда я поверну назад–сказала Точка.– Я, наверное, пошла не в ту сторону. (Слайд 11)
–Сможет ли Точка найти концы прямой? (Нет)
Без конца и края
Линия прямая!
Хоть сто лет по ней идти
Не найти конца пути!
–Опечалилась Точка. Что же, так и идти без конца? Вдруг Точка решила: « А что, если я позову на помощь Ножницы. Тут, откуда ни возьмись, появились Ножницы; щёлкнули перед самым Точкиным носом и разрезали прямую.
–Ура!– закричала Точка.- Вот и конец получился! Ай да Ножницы! А теперь сделайте, пожалуйста, конец с другой стороны.
–Можно и с другой, — послушно щёлкнули Ножницы. (Слайд12)
–Как интересно!– воскликнула Точка. — Что же из моей прямой получилось? С одной стороны конец, с другой стороны конец.
–Ребята, как называется эта фигура? (отрезок)
–Отрезок!– с удовольствием повторила Точка, прогуливаясь по отрезку от одного конца до другого.
–Ребята, а чем отрезок отличается от прямой? (имеет концы)
– Я запомню это название. Мне нравится отрезок. Здесь я устрою свой дом. Но прямая мне тоже нравилась. Жаль, что её не стало. Ведь теперь вместо прямой есть мой отрезок и ещё два этих ….не знаю, как их назвать. У них конец только с одной стороны, а в другую сторону нет конца.
– Как они называются? (Лучи)
– А!– радостно сказала Точка.– Я знаю, почему они так называются. Они похожи на солнечные лучики. Начинаются на солнце и идут без конца, если только не встретят что-нибудь на своём пути.
–Чем луч отличается от отрезка? От прямой?
Показ слайда с фигурами (слайд 13)
– Что вы здесь видите?
- Назовите прямые
- Назовите лучи
- Назовите отрезки
IV.Закрепление.
–Точка предлагает нам рассмотреть упражнения в учебнике.
№2, стр.7. Задание выполняется под руководством учителя.
№3, стр.7. Самостоятельно. Проверка фронтально.
№6, стр.8 Работа в парах с взаимопроверкой. (Слайд 14)
V. Повторение.
Точка довольна тем, как мы выполнили задания с геометрическими фигурами. А теперь давайте покажем, как мы умеем решать задачи.
№8, стр.8– Решение самостоятельное с последующей проверкой на (Слайде 15)
Задание усложняется.
№10,стр. 9– Разбор и решение задачи под руководством учителя.
№15, стр.9– Самостоятельная работа на сложение и вычитание трёхзначных чисел.
Проверка (Слайд16)
Комментарий к «Суздаль»
Исторический центр города Суздаля, окруженный насыпными земляными валами, сохранившимися и по сей день, и его сердце — Суздальский Кремль, в одной из многочисленных экспозиций которого Вы найдёте миниатюрный макет города Суздаля, каким он был сотни лет назад…
Монастыри, храмы и соборы Суздаля — одни из самых ярких памятников архитектуры города, но кроме них есть ещё и другие, не менее заметные и значимые — такие, как торговые ряды на центральной (“торговой”) площади Суздаля, и сама торговая площадь, вымощенная старинным булыжником, с ансамблем церквей на заднем плане — излюбленное место для фотографирования…
VI.Итог урока.
- Путешествие, в какую страну мы сегодня совершили?
- С какими фигурами встретились на уроке?
- Чем отличается отрезок от прямой?
- Что вы можете сказать про луч?
(Слайд 17)
VII. Домашнее задание. Стр.8, №7, №14.
Тезис:
Урок математики 2 класса,.» «Прямая. Луч. Отрезок» Урок помогает закрепить представления о понятиях «прямая», «луч», «отрезок», распознавать их, находить и обозначать точки пересечения. На уроке отрабатываются вычислительные навыки
Источник: https://infourok.ru/tema-pryamaya-luch-otrezok-648942.html
Плоскость. Прямая. Луч

Давайте представим себе такую историю.
В математике она
Пригождается всегда:
Без хвоста от запятой
Всем нам кажется простой.
И в конце, закончив строчку,
Мы поставим, братцы…
– Ну это легкотня! Это же точка! — обрадовался Саша.
– Саша, а что ты делаешь? — спросил Паша.
– Нам по математике задали разгадать загадки.
– А можно я с тобой вместе поразгадываю? — спросил Паша.
– Конечно! — обрадовался Саша, — вместе же интереснее. И ребята принялись читать загадки.
Линию прямую, ну-ка,
Сам нарисовать сумей-ка!
Это сложная наука!
Пригодится здесь…
– Линейка! — обрадовался Паша. Давай следующую загадку.
Он ограничен с двух сторон
И по линейке проведён.
Длину его измерить можно,
И сделать это так несложно!
– Я знаю, что это! — обрадовался Саша, — это отрезок! Помнишь, нам Электроша о нём рассказывал? Давай читать следующую загадку.
Он от солнца прилетает,
Пробивая толщу туч,
И в тетрадочке бывает,
А зовётся просто…
– Эта загадка уже посложнее, — задумался Саша.
– Смотри! — воскликнул Паша, — если внимательно читать эту загадку, то там в начале говорится, что он прилетает от солнца сквозь толщу туч. Мне кажется, я догадался… это же луч!
– Точно! — обрадовался Саша, — но в загадке говорится, что он бывает и в тетрадке. Как луч может оказаться в тетрадке?
– Не знаю, — задумался Паша, — но точно знаю, кто может нам помочь!
– Ребята, прежде чем я вас познакомлю с ещё несколькими геометрическими фигурами, хочу, чтобы вы немного размялись и выполнили устные задания, — предложил Электроша.
– Давайте сверимся! — сказал Электроша. — Посмотрите, что у вас должно было получиться!
– Ну а теперь самое время познакомить вас с такими геометрическими фигурами, как луч и прямая, — начал Электроша, — но сначала вам нужно усвоить ещё кое-какое понятие. Мы с вами уже научились строить отрезки в тетради. Но скажите, на сколько большой отрезок вы сможете построить в своей тетради? — спросил он у ребят.
– Самый большой отрезок в тетради получится, если чертить его, начиная с одного угла листа и заканчивая в противоположном ему углу, — предположил Паша.
– Да, — согласился Электроша. Как видите, размеры тетради ограничивают нас и не дают нам строить отрезки очень большой длины. А давайте попробуем представить себе, что тетрадный лист с помощью волшебного заклинания вырос до размеров поверхности стола. Длина вашего большого отрезка как-то поменялась?
– Да! — воскликнули мальчишки, — он стал ещё больше!
– А теперь представьте себе, что этот тетрадный лист стал ещё больше, например, размером с футбольное поле. Что стало с длиной вашего отрезка? — спросил ребят Электроша.
– Он стал огромным! — представляли отрезок мальчишки.
Поверхности тетрадного листа, стола, футбольного поля дают нам представление о плоскости, — продолжил Электроша. Только эти поверхности имеют границы, а плоскость в математике безгранична во всех направлениях.
Запомните! Плоскость бесконечна. Поэтому эту геометрическую фигуру нельзя изобразить, но её можно вообразить.
– А значит, на плоскости можно начертить отрезок очень большой длины? — решил спросить Паша.
– И не только, — ответил Электроша. Вот давайте построим отрезок АВ. Напоминаю, что отрезок — это кратчайшая линия, соединяющая две точки.
Если этот отрезок с помощью линейки продлить в обе стороны, то мы получим ещё одну геометрическую фигуру, которую называют прямой.
– А где прямая заканчивается? — спросил Саша.
– Ребята, запомните! — сказал Электроша, — прямая не имеет концов. Она бесконечна. Поэтому на рисунке мы можем изобразить только часть прямой, но мысленно мы должны понимать, что прямая продолжается в обе стороны бесконечно.
– А теперь давайте отметим на листе бумаги две точки — А и В. Проведём через них прямую. А теперь попробуйте через эти же две точки провести ещё одну прямую. Получается?
– Нет, — задумались мальчишки.
– Запомните! — сказал Электроша. — Через любые две точки проходит одна единственная прямая.
Это свойство позволяет обозначать прямую, называя две любые её точки. Так, например, прямую, которую мы с вами сейчас построили, обозначают одним из двух способов: АВ или ВА. А читают: «прямая АВ» или «прямая ВА». Точки А и В лежат на прямой.
Но иногда прямые обозначают одной строчной латинской буквой. Посмотрите, на листе я построил две прямые: прямую m и прямую n.
Любая прямая делит плоскость на две части, на две полуплоскости.
– Электроша, а что это за фигура, которая называется лучом? — решили спросить мальчишки, вспомнив о своей загадке.
– Сейчас я вам объясню, — сказал Электроша.
Давайте построим прямую АВ и отметим на ней точку О. Посмотрите, эта точка разделила нашу прямую на две части. Каждую их этих частей называют лучом с началом в точке О. Конца у луча нет.
– То есть луч имеет начало, но не имеет конца? — спросил Паша.
– Правильно! — ответил Электроша. — Геометрический луч очень похож на световой, поэтому его так и назвали. Чтобы лучше представить себе луч, вспомним лазерную указку. Вспомнили? Луч света начинается в лазерной указке и уходит в бесконечность по прямой.
– Теперь понятно, — сказал Паша.
– А как обозначают лучи в математике? — спросил Саша.
– Так же, как и прямую, — ответил Электроша. — Луч обозначают двумя прописными буквами, только сначала записывают букву, которая обозначает начало луча, а потом букву, обозначающую какую-либо другую точку этого луча.
Так, в нашем примере, точка О делит прямую АВ на два луча: луч ОА и луч ОВ. Переставлять буквы в названии луча нельзя. Первой буквой всегда обозначается начало луча.
Лучи, на которые точка разбивает прямую, называют дополнительными друг другу.
И, кстати, луч — это ещё один пример геометрической фигуры.
– Запомните, ребята, в отличие от прямой, луч бесконечен только в одну сторону.
– Электроша, я совсем запутался, — перебил Электрошу Саша, — отрезок, прямая, луч — они такие все одинаковые, чертятся прямой линией, обозначаются буквами…
– Сейчас я вам покажу, чем они отличаются, и вы быстренько их запомните, — сказал Электроша. — Отрезок, луч, прямая являются прямыми линиями. А различаются они наличием концов. Запомните! У отрезка два конца, у луча — один, а у прямой нет ни одного.
– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.
Задание первое: назовите фигуры, изображённые на рисунке.
Решение: на рисунке изображены отрезки АВ, АК и КВ; лучи АК, ВА, КА, КВ; прямая АВ.
Следующее задание. Ответить на вопрос: пересекаются ли изображённые на рисунке фигуры?
Решение: сначала мы должны ответить на вопрос о том, пересекаются ли прямая MN и прямая ЕF. Так как прямая бесконечна, то видим, что эти две прямые пересекаются. Теперь посмотрим, пересекаются ли отрезки MN и ЕF.
Так как отрезок — это кратчайшая линия, соединяющая две точки, то наши отрезки не пересекаются. Далее посмотрим, пересекаются ли луч NM и луч FЕ. Помним, что луч имеет начало, но не имеет конца. И первой буквой обозначают начало луча. Значит, наши лучи пересекаются.
И посмотрим ещё, пересекаются ли луч ЕF и луч MN. Точки Е и M — это начала наших лучей. Значит, лучи не пересекаются.
– Ребята, вы отлично справляетесь с заданиями! — с радостью сказал Электроша. — А значит, вы обязательно справитесь с моей непростой задачей.
Итак, из террариума сбежали 4 гадюки, 5 кобр и 8 гремучих змей. Длина каждой гадюки — 1 метр, каждой кобры — 1 метр 4 сантиметра, а каждой гремучей змеи — 2 метра 35 сантиметров. Сколько метров ядовитых змей сбежало из террариума?
Решение: для начала нужно перевести длину каждой змеи в одну единицу измерения. Будем переводить в сантиметры. Мы знаем, что 1 м = 100 см. Тогда длина одной гадюки равна 100 см, длина одной кобры 104 см, длина одной гремучей змеи — 235 см.
Далее найдём длины всех змей каждой разновидности. Т.к. гадюк по условию сбежало 4, то длина всех гадюк в совокупности равна: 4 умножить на 100, то есть 400 см. Длина 5 кобр равна: 5 умножить на 104, то есть 520 см.
И длина 8 гремучих змей равна: 8 умножить на 235, то есть 1880 см. Теперь, зная длины всех сбежавших змей, можем найти длину всех змей в совокупности. Тогда получим: 400 + 520 + 1880, то есть 2800 см.
Так как в вопросе задачи сказано, что необходимо найти, сколько метров ядовитых змей сбежало из террариума, то нужно перевести 2800 см в метры. Значит, получим 28 метров.
Ответ: 28 метров ядовитых змей сбежало из террариума.
Источник: https://videouroki.net/video/04-ploskost-pryamaya-luch.html
Понятие луча в геометрии: понятие, как начертить и обозначить, отличие от светового
Главная> Наука> Математика> Как объяснить, что такое луч в геометрии
Все мы когда-то изучали в школе геометрию, но далеко не каждый из нас вспомнит, что представляет собой отрезок. А уж тем более мало кто сможет объяснить понятие лучей, и как они обозначаются.
Давайте постараемся в этой статье напомнить себе данные определения и рассмотрим их в математике. Также определим, что такое луч, и чем он отличается от светового.
Если вникнуть, то понять будет несложно.
Определение понятий
Для начала давайте вспомним, что называется геометрией. Геометрия — это раздел математики, изучающий геометрические фигуры и их свойства. К ним относятся треугольник, квадрат, прямоугольник, параллелепипед, круг, овал, ромб, цилиндр и т. п.
Простейшая фигура — это прямая. Она является бесконечной и не имеет начала. Две прямые пересекутся только в одной единственной точке. Через одну точку можно проводить бессчетное количество прямых линий.
Каждая точка на линии делит ее на два.
Открытый луч
Он состоит из точек, расположенных по одну сторону. Все понятия данных подмножеств можно именовать таким образом. Луч обозначают одной строчной латинской буквой или двумя заглавными, когда одна точка — начало (например, О), а вторая лежит на нем (например, F, К и Е) .
В основе геометрической фигуры, имеющей углы, лежат полупрямые. Они начинаются в точке, где пересекаются, но второй стороной направлены в бесконечность. Начало делит прямую на 2 части.
На письме его обычно именуют двумя заглавными (OF) или одной буквой латиницы (а, в, с). Если дана прямая, то записывается ОВ в закругленных скобках: (ОВ).
Если же это отрезок — в квадратных скобках.
Таким образом, луч — это часть прямой. Через любую точку можно провести множество прямых, но через 2 несовпадающие — только одну. Последние могут быть взаимодействовать только в трех вариантах: пересекаться, скрещиваться, быть параллельными друг другу. Существуют линейные уравнения, которые задают прямую на плоскости.
Обозначения в геометрии
Вариантов для обозначения несколько:
- Попробуйте провести на тетрадном листе линию. Представим, что у вас имеется полупрямая «О». Точка О — исходная, другой быть не может. Это самый распространенный способ.
- Данный метод более интересен: нашу полупрямую возможно назвать не одной буквой. К примеру, на одной линии может быть их две, где первая — начало (буква О), а вторая расположена на каком-то расстоянии. Представим, что на отрезке длиной 10 сантиметров начало названо буквой О, а на расстоянии четырех сантиметров от (О) находится вторая точка (В). Тогда его обозначают «ОВ».
- Третий способ — это когда О у нас располагается не в начале, а с каким-то отступом. Итак, снова начертите прямую с длиной десять сантиметров, отступите слева один сантиметр и отметьте начало. Снова назовите буквой О. В центре точку не ставьте, но обозначьте данную область буквой К. В этот раз буква О — это его начало. Название читается как «ОК»:
- Для начала начертим дополняющие лучи. Как мы уже разобрались, на прямой нужно поставить точку (называем ее О), она производная и разделяет ее на 2 линии, которые пересечься не могут.
- Перейдем к следующему этапу. Теперь нам нужно начертить продолжение — линию, имеющую общее начало с основополагающей, но не совпадающей с нею. А именно: дополняющая линия не является продолжением.
- Чтоб начертить продолжение, проведем из О прямую, которая не располагается на дополняющих, но имеет с ними одно начало. После того как начертили, отметим на новом луче точку В. ОВ теперь лежит на его продолжении из О.
Отличие световых лучей от геометрических
В геометрии таковые понятия очень схожи. Луч — это линия, но она является энергией света. Другими словами — это небольшой пучок света.
В оптике данное понятие, как и понятие прямой, в геометрии — базовое. У световых нет сконцентрированного направления, происходит дифракция.
Но когда поток света очень сильный, расходимостью пренебрегают, и можно выделять четкое направление.
Отзывы и комментарии
Источник: https://obrazovanie.guru/nauka/matematika/kak-obyasnit-chto-takoe-luch-v-geometrii.html




