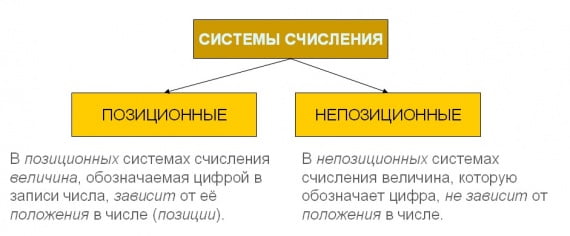
Позиционные и непозиционные системы счисления
Разнообразные системы счисления, которые существовали раньше и которые используются в наше время, можно разделить на непозиционные и позиционные системы счисления. Знаки, используемые при записи чисел, называются цифрами.
В непозиционных системах счисления от положения цифры в записи числа не зависит величина, которую она обозначает. Примером непозиционной системы счисления является римская система, в которой в качестве цифр используются латинские буквы: I V X L C D M
1 5 10 50 100 500 1000
В числе цифры записываются слева направо в порядке убывания. Величина числа определяется как сумма или разность цифр в числе. Если меньшая цифра стоит слева от большей цифры, то она вычитается, если справа — прибавляется. Например, VI = 5 + 1 = 6, а IX = 10 — 1 = 9, СССXXVII=100+100+100+10+10+5+1+1=327.
В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции. Количество используемых цифр называется основанием системы счисления. Место каждой цифры в числе называется позицией. Система счисления Основание Алфавит
Десятичная 10 0123456789
Двоичная 2 01
Троичная 3 012
Восьмеричная 8 01234567
Шестнадцатеричная 16 0123456789ABCDEF
Первая известная нам система, основанная на позиционном принципе — шестидесятеричная вавилонская. Цифры в ней были двух видов, одним из которых обозначались единицы, другим — десятки. Следы вавилонской системы сохранились до наших дней в способах измерения и записи величин углов и промежутков времени.
Однако наибольшую ценность для нас имеет индо-арабская десятичная система. Индийцы первыми использовали ноль для указания позиционной значимости величины в строке цифр. Эта система получила название десятичной системы счисления, так как в ней десять цифр.
Для того чтобы лучше понять различие позиционной и непозиционной систем счисления, рассмотрим пример сравнения двух чисел. В позиционной системе счисления сравнение двух чисел происходит следующим образом: в рассматриваемых числах слева направо сравниваются цифры, стоящие в одинаковых позициях.
Большая цифра соответствует большему значению числа. Например, для чисел 123 и 234, 1 меньше 2, поэтому число 234 больше, чем число 123. В непозиционной системе счисления это правило не действует. Примером этого может служить сравнение двух чисел IX и VI.
Несмотря на то, что I меньше, чем V, число IX больше, чем число VI.
Далее мы будем рассматривать только позиционные системы счисления.
Основание системы счисления, в которой записано число, обычно обозначается нижним индексом. Например, 5557 — число, записанное в семеричной системе счисления. Если число записано в десятичной системе, то основание, как правило, не указывается.
Основание системы — это тоже число, и его мы будем указывать в обычной десятичной системе. Вообще, число x может быть представлено в системе с основанием p, как x=an*pn+an-1*pn-1+ a1*p1+a0*p0, где an…a0 — цифры в представлении данного числа.
Так, например, 103510=1*103+0*102+3*101+5*100;
10102 = 1*23+0*22+1*21+0*20 = 10.
Наибольший интерес при работе на ЭВМ представляют системы счисления с основаниями 2, 8 и 16. Вообще говоря, этих систем счисления обычно хватает для полноценной работы, как человека, так и вычислительной машины. Однако иногда в силу различных обстоятельств приходится обращаться к другим системам счисления, например, к троичной, семеричной или системе счисления по основанию 32.
Для того чтобы нормально оперировать с числами, записанными в таких нетрадиционных системах, важно понимать, что принципиально они ничем не отличаются от привычной нам десятичной системы счисления. Сложение, вычитание, умножение в них осуществляется по одной и той же схеме.
Почему же мы не пользуемся другими системами счисления? В основном потому, что в повседневной жизни мы привыкли пользоваться десятичной системой счисления, и нам не требуется никакая другая система счисления. В вычислительных же машинах используется двоичная система счисления, так как оперировать над числами, записанными в двоичном виде, довольно просто.
Часто в информатике используют шестнадцатеричную систему, так как запись чисел в ней значительно короче записи чисел в двоичной системе.
Может возникнуть вопрос: почему бы не использовать для записи очень больших чисел систему счисления, например по основанию 50? Для такой системы счисления необходимы 10 обычных цифр плюс 40 знаков, которые соответствовали бы числам от 10 до 49 и вряд ли кому-нибудь понравится работать с этими сорока знаками. Поэтому в реальной жизни системы счисления по основанию, большему 16, практически не используются.
Методику представления информации в двоичной форме можно пояснить, проведя следующую игру. Нужно у собеседника получить интересующую нас информацию, задавая любые вопросы, но получая в ответ только одно из двух ДА либо НЕТ. Известным способом получения во время этого диалога двоичной формы информации является перечисление всех возможных событий.
Рассмотрим простейший случай получения информации. Вы задаете только один вопрос: Идет ли дождь?. При этом условимся, что с одинаковой вероятностью ожидаете ответ: ДА или НЕТ. Легко увидеть, что любой из этих ответов несет самую малую порцию информации. Эта порция определяет единицу измерения информации, называемую битом.
Благодаря введению понятия единицы информации появилась возможность определения размера любой информации числом битов. Образно говоря, если, например, объем грунта определяют в кубометрах, то объем информации — в битах. Условимся каждый положительный ответ представлять цифрой 1, а отрицательный — цифрой 0.
Тогда запись всех ответов образует многозначную последовательность цифр, состоящую из нулей и единиц, например 0100.
Люди предпочитают десятичную систему, вероятно, потому, что с древних времен считали по пальцам. Но, не всегда и не везде люди пользовались десятичной системой счисления. В Китае, например, долгое время применялась пятеричная система счисления. В ЭВМ используют двоичную систему потому, что она имеет ряд преимуществ перед другими:
для ее реализации используются технические элементы с двумя возможными состояниями (есть ток — нет тока, намагничен — ненамагничен);
представление информации посредством только двух состояний надежно и помехоустойчиво;
возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
двоичная арифметика проще десятичной (двоичные таблицы сложения и умножения предельно просты).
В двоичной системе счисления всего две цифры, называемые двоичными (binary digits). Сокращение этого наименования привело к появлению термина бит, ставшего названием разряда двоичного числа. Веса разрядов в двоичной системе изменяются по степеням двойки.
Поскольку вес каждого разряда умножается либо на 0, либо на 1, то в результате значение числа определяется как сумма соответствующих значений степеней двойки. Если какой-либо разряд двоичного числа равен 1, то он называется значащим разрядом.
Запись числа в двоичном виде намного длиннее записи в десятичной системе счисления.
Арифметические действия, выполняемые в двоичной системе, подчиняются тем же правилам, что и в десятичной системе. Только в двоичной системе счисления перенос единиц в старший разряд возникает чаще, чем в десятичной. Вот как выглядит таблица сложения в двоичной системе: 0 + 0 = 0 0 + 1 = 1
1 + 0 = 1 1 + 1 = 10 (перенос в старший разряд)
Таблица умножения для двоичных чисел еще проще: 0 * 0 = 0 1 * 0 = 0 0 * 1 = 0 1 * 1 = 1
Рассмотрим подробнее, как происходит процесс умножения двоичных чисел. Пусть надо умножить число 1101 на 101 (оба числа в двоичной системе счисления).
Машина делает это следующим образом: она берет число 1101 и, если первый элемент второго множителя равен 1, то она заносит его в сумму.
Затем сдвигает число 1101 влево на одну позицию, получая тем самым 11010, и если, второй элемент второго множителя равен единице, то тоже заносит его в сумму. Если элемент второго множителя равен нулю, то сумма не изменяется.
Двоичное деление основано на методе, знакомом вам по десятичному делению, т. е. сводится к выполнению операций умножения и вычитания. Выполнение основной процедуры — выбор числа, кратного делителю и предназначенного для уменьшения делимого, здесь проще, так как таким числом могут быть только либо 0, либо сам делитель.
Следует отметить, что большинство калькуляторов, реализованных на компьютере, позволяют осуществлять работу в системах счисления с основаниями 2, 8, 16 и, конечно, 10.
При наладке аппаратных средств компьютера или создании новой программы возникает необходимость заглянуть внутрь памяти машины, чтобы оценить ее текущее состояние. Но там все заполнено длинными последовательностями нулей и единиц двоичных чисел.
Эти последовательности очень неудобны для восприятия человеком, привыкшим к более короткой записи десятичных чисел.
Кроме того, естественные возможности человеческого мышления не позволяют оценить быстро и точно величину числа, представленного, например, комбинацией из 16 нулей и единиц.
Для облегчения восприятия двоичного числа решили разбивать его на группы разрядов, например, по три или четыре разряда. Эта идея оказалась очень удачной, так как последовательность из трех бит имеет 8 комбинаций, а последовательность из 4 бит — 16.
Числа 8 и 16 являются степенями двойки, поэтому легко находить соответствие с двоичными числами. Развивая эту идею, пришли к выводу, что группы разрядов можно закодировать, сократив при этом длину последовательности знаков.
Для кодировки трех битов требуется восемь цифр, поэтому взяли цифры от 0 до 7 десятичной системы. Для кодировки же четырех битов необходимо шестнадцать знаков; для этого взяли 10 цифр десятичной системы и 6 букв латинского алфавита: A, B, C, D, E, F.
Полученные системы, имеющие основания 8 и 16, назвали соответственно восьмеричной и шестнадцатеричной.
В восьмеричной (octal) системе счисления используются восемь различных цифр 0, 1, 2, 3, 4, 5, 6, 7. Основание системы — 8. При записи отрицательных чисел перед последовательностью цифр ставят знак минус.
Сложение, вычитание, умножение и деление чисел, представленных в восьмеричной системе, выполняются весьма просто подобно тому, как это делают в общеизвестной десятичной системе счисления.
В различных языках программирования запись восьмеричных чисел начинается с 0, например, запись 011 означает число 9.
В шестнадцатеричной (hexadecimal) системе счисления применяется десять различных цифр и шесть первых букв латинского алфавита. При записи отрицательных чисел слева от последовательности цифр ставят знак минус.
Для того чтобы при написании компьютерных программ отличить числа, записанные в шестнадцатеричной системе, от других, перед числом ставят 0x. То есть 0x11 и 11 — это разные числа.
В других случаях можно указать основание системы счисления нижним индексом.
Шестнадцатеричная система счисления широко используется при задании различных оттенков цвета при кодировании графической информации (модель RGB). Так, в редакторе гипертекста Netscape Composer можно задавать цвета для фона или текста как в десятичной, так и шестнадцатеричной системах счисления.
Статьи к прочтению:
Источник: http://csaa.ru/pozicionnye-i-nepozicionnye-sistemy-schislenija/
Позиционные и непозиционные системы счисления

Системой счисления называют систему приемов и правил, позволяющих устанавливать взаимнооднозначное соответствие между любым числом и его представлением в виде совокупности конечного числа символов. Множество символов, используемых для такого представления, называют цифрами.
Системы счисления делятся на два класса позиционные и непозиционные. В непозиционных системах любое число определяется как некоторая функция от численных значений совокупности цифр, представляющих это число. Простейшая, но абсолютно неудобная система счисления.
Основана на единственной цифре — единице (палочке). Позволяет записывать только натуральные числа. Чтобы представить число в этой системе счисления нужно записать столько палочек, каково само число.
Использовалась нецивилизованными племенами, потребности которых в счете, как правило, не выходили за рамки первого десятка.
В Римской системе счисления с помощью семи цифр — I=1 , V=5 , X=10 , L=50 , C=100 , D=500 , M=1000 — можно весьма успешно и довольно выразительно представлять натуральные числа в диапазоне до нескольких тысяч.
Исторически первыми системами счисления были именно непозиционные системы. Одним из основных недостатков является трудность записи больших чисел.
Запись больших чисел в таких системах либо очень громоздка, либо алфавит системы чрезвычайно велик.
В вычислительной технике непозиционные системы не применяются, но продолжают ограниченно использоваться для указания порядковых числительных (часов, столетий, номеров съездов или конференций и т.п.).
Позиционная система счисления — система счисления, в которой вес цифры меняется с изменением положения цифры в числе, но при этом полностью определяется написанием цифры и местом, которое она занимает. В частности, это означает, что вес цифры не зависит от значений окружающих ее цифр.
Такая система счисления основывается на том, что некоторое число n единиц ( основание системы счисления ) объединяются в одну единицу второго разряда, n единиц второго разряда объединяются в одну единицу третьего разряда и т. д. Основанием систем счисления может быть любое число, больше единицы.
К числу таких систем относится современная десятичная система счисления ( с основанием n=10 ). В ней для обозначения первых десяти чисел служат цифры 0,1,…,9. Несмотря на кажущуюся естественность такой системы, она явилась результатом длительного исторического развития.
Возникновение десятичной системы счисления связывают со счетом на пальцах. В отличии от непозиционной системы счисления, позиционная система счисления применяется в ЭВМ.
Двоичная система счисления в настоящий момент наиболее употребительная в информатике, вычислительной технике и смежных отраслях, использующая две цифры — 0 и 1. Для представления этих чисел в цифровых системах достаточно иметь электронные схемы, которые могут принимать два состояния, четко различающиеся значением какой-либо электрической величины — потенциала или тока.
Одному из значений этой величины соответствует цифра 0, другому 1. Относительная простота создания электронных схем с двумя электрическими состояниями и привела к тому, что двоичное представление чисел доминирует в современной цифровой технике. При этом 0 обычно представляется низким уровнем потенциала, а 1 — высоким уровнем. Такой способ представления называется положительной логикой.
История развития двоичной системы счисления — одна из ярких страниц в истории арифметики. Официальное «рождение» двоичной арифметики связывают с именем Г. В. Лейбница, опубликовавшего статью, в которой были рассмотрены правила выполнения всех арифметических операций над двоичными числами.
До начала тридцатых годов XX века двоичная система счисления оставалась вне поля зрения прикладной математики.
Потребность в создании надежных и простых по конструкции счетных механических устройств и простота выполнения действий над двоичными числами привели к более глубокому и активному изучению особенностей двоичной системы как системы, пригодной для аппаратной реализации.
Первые двоичные механические вычислительные машины были построены во Франции и Германии. Утверждение двоичной арифметики в качестве общепринятой основы при конструировании ЭВМ с программным управлением состоялось под несомненным влиянием работы А. Бекса, Х. Гольдстайна и Дж.
Фон Неймана о проекте первой ЭВМ с хранимой в памяти программой, написанной в 1946 году. В этой работе наиболее аргументировано обоснованы причины отказа от десятичной арифметики и перехода к двоичной системе счисления как основе машинной арифметики.
Восьмеричная система счисленияиспользует восемь цифр — 0, 1, 2, 3, 4, 5, 6, и 7. Широко использовалась в программировании в 1950-70-ые гг. К настоящему времени практически полностью вытеснена шестнадцатеричной системой счисления, однако функции перевода числа из десятичной системы в восьмеричную и обратно сохраняются в микрокалькуляторах и многих языках программирования.
Десятеричная система счисленияиспользует десять обычных цифр — 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Существует массовое заблуждение, будто именно десятичная система счисления является наиболее употребительным способом записи чисел.
Между тем, более внимательный анализ правил чтения и записи чисел приводит к другому выводу: система счисления, которой мы обычно пользуемся, фактически является двойной, так как имеет основания — 10 и 1000.
В частности, в русском языке известны названия только для первых семи разрядов десятичной системы счисления ( 1 — единица, 10 — десяток, 100 — сотня, 1000 — тысяча, 10000 — тьма, 100000 — легион, 1000000 — миллион ), но предпоследние два из них (легион и тьма) давно вышли из употребления, а соседние с ними (миллион и тысяча) — названия классов, а не только разрядов. Итак, фактически в русском языке остались лишь два самостоятельных названия для десятичных разрядов: десяток и сотня. В других языках — аналогичная ситуация.
Шестнадцатеричная система счисленияиспользует шестнадцать цифр — 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 в их обычном смысле, а затем A=10, B=11 , C=12 , D=13 , E=14 , F=15 . Также использует символы «+» и «–» для обозначения знака числа и запятую (точку) для разделения целой и дробной частей числа. Внедрена американской корпорацией IBM.
Широко используется в программировании для IBM-совместимых компьютеров. С другой стороны, в некоторых языках сохранились и следы использования этой системы счисления в прошлом. Например, в романских языках (испанском, французском и др.) числительные от 11 до 16 образуются по одному правилу, а от 17 до 19 — по другому.
А в русском языке известен пуд, равный 16 килограммам.
Источник: https://cyberpedia.su/17xec42.html
Позиционные и непозиционные системы счисления

Обратная связь
ПОЗНАВАТЕЛЬНОЕ
Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса — ваш вокал
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший “Салат из свеклы с чесноком”
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Системой счисления называется совокупность приемов и правил представления чисел с помощью цифровых знаков.
Непозиционной называется такая система счисления, в которой значение любой цифры не зависит от положения (позиции) в ряду цифр, изображающих это число.
Например, в числе ХХХ, записанном в римской системе счисления, каждый разряд означает 10 единиц.
Задача 1. Записать числа в римской нумерации: а) 193; б) 564; в) 2708.
Решение: а) 193 — это сто (С) + девяносто, т.е. сто без десятка (ХС) + три (III). Следовательно, 193 запишется как СХСIII.
б) 564 — это пятьсот (D) + пятьдесят (L) + десять (Х) + четыре (IV), т.е. число 564 запишется как DLХIV.
в) 2708 — это две тысячи (ММ) + плюс пятьсот (D) + сто (С) + сто (С) + пять (V) + три (III). Следовательно, число 2708 записывается так: ММDCCVIII.
Позиционной называется такая система счисления, в которой значение любой цифры зависит от ее положения (позиции) в ряду цифр, изображающих это число.
Например, цифра 3 в числе 723, записанном в десятичной системе счисления, означает три единицы, а в числе 325 — три сотни. К позиционным СС можно отнести шестидесятиричную вавилонскую и десятичную системы счисления.
Под основанием системы счисления понимается определенное постоянное для данной системы счисления отношение единиц соседних разрядов.
Основанием системы счисления может быть любое натуральное число большее 1.
Система счисления с основанием равным 1 называется унарной.
Для записи чисел в позиционной системе счисления используются цифры, количество которых соответствует основанию системы.
Десятичная система счисления, запись чисел в ней
В практике установилась десятичная система счисления. Как известно, в десятичной СС для записи чисел используются 10 знаков (цифр): 1,2,3,4,5,6,7,8,9,0. Из них образуются конечные последовательности, которые являются краткими записями чисел. Например, последовательность 3745 является краткой записью числа.
Определение 4.Десятичной записью натурального числа xназывается его представление в виде:
,
где коэффициенты an, an-1, …, a1, a0 принимают значения 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и
Суммув краткой форме принято записывать последовательностью цифр с чертой наверху, чтобы отличать от произведения чисел:
.
Так как понятие числа и его записи нетождественны, то существование и единственность десятичной записи натуральной записи надо доказывать.
Теорема 1. Любое натуральное число х можно представить в виде:
(1)
где коэффициенты an, an-1, …, a1, a0 принимают значения 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
и такая запись единственная.
Десятичная запись числа позволяет просто решать вопрос о том, какое из них меньше.
Теорема 2. Пусть х и у — натуральные числа, запись которых дана в десятичной системе счисления:
.
Тогда число х меньше числа у, если выполнено одно из условий:
а) n
Источник: https://megapredmet.ru/1-69178.html
Системы счисления

Системы счисления (нумерация) — совокупность способов обозначения натуральных чисел.
На ранних ступенях развития общества люди почти не умели считать. Они различали совокупности двух и трех предметов; всякая совокупность, содержавшая бóльшее число предметов, объединялась в понятии «много». Предметы при счете сопоставлялись обычно с пальцами рук и ног.
По мере развития цивилизации потребность человека в счете стала необходимой. Первоначально натуральные числа изображались с помощью некоторого количества черточек или палочек, затем для их изображения стали использовать буквы или специальные знаки.
В древнем Новгороде использовалась славянская система, где применялись буквы славянского алфавита; при изображении чисел над ними ставился знак ~ (титло).
Древние римляне пользовались нумерацией, сохраняющейся до настоящего времени под именем «римской нумерации», в которой числа изображаются буквами латинского алфавита. Сейчас ею пользуются для обозначения юбилейных дат, нумерации некоторых страниц книги (например, страниц предисловия), глав в книгах, строф в стихотворениях и т.д. В позднейшем своем виде римские цифры выглядят так:
I = 1; V = 5; X = 10; L = 50; С = 100; D = 500; M = 1000.
О происхождении римских цифр достоверных сведений нет. Цифра V могла первоначально служить изображением кисти руки, а цифра Х могла составиться из двух пятерок. В римской нумерации явственно сказываются следы пятеричной системы счисления. Все целые числа (до 5000) записываются с помощью повторения вышеприведенных цифр.
При этом, если бóльшая цифра стоит перед меньшей, то они складываются, если же меньшая стоит перед бóльшей (в этом случае она не может повторяться), то меньшая вычитается из бóльшей). Например, VI = 6, т.е. 5 + 1, IV = 4, т.е. 5 — 1, XL = 40, т е. 50 — 10, LX = 60, т.е. 50 + 10.
Подряд одна и та же цифра ставится не более трех раз: LXX = 70; LXXX = 80; число 90 записывается ХС (а не LXXXX).
Первые 12 чисел записываются в римских цифрах так:
I, II, III, IV, V, VI, VII, VIII. IX, X, XI, XII.
Другие же числа записываются, например, как:
XXVIII = 28; ХХХIХ = 39; CCCXCVII = 397; MDCCCXVIII = 1818.
Выполнение арифметических действий над многозначными числами в этой записи очень трудно. Тем не менее, римская нумерация преобладала в Италии до 13 в., а в других странах Западной Европы — до 16 в.
В славянской системе нумерации для записи чисел использовались все буквы алфавита, правда, с некоторым нарушением алфавитного порядка. Различные буквы означали различное количество единиц, десятков и сотен. Например, число 231 записывалось в виде ~ СЛА (C — 200, Л — 30, А — 1).
Этим системам свойственны два недостатка, которые привели к их вытеснению другими: необходимость большого числа различных знаков, особенно для изображения больших чисел, и, что еще важнее неудобство выполнения арифметических операций.
Более удобной и общепринятой и наиболее распространенной является десятичная система счисления, которая была изобретена в Индии, заимствована там арабами и затем через некоторое время пришла в Европу. В десятичной системе счисления основанием является число 10.
Существовали системы исчисления и с другими основаниями. В Древнем Вавилоне, например, применялась шестидесятеричная система счисления. Остатки ее мы находим в сохранившемся до сих пор делении часа или градуса на 60 минут, а минуты — на 60 секунд.
Широкое распространение имела в древности и двенадцатеричная система, происхождение которой, вероятно, связано, как и десятичной системы, со счетом на пальцах: за единицу счета принимались фаланги (отдельные суставы) четырех пальцев одной руки, которые при счете перебирались большим пальцем той же руки.
Остатки этой системы счисления сохранились и до наших дней и в устной речи, и в обычаях. Хорошо известно, например, название единицы второго разряда — числа 12 — «дюжина».
Сохранился обычай считать многие предметы не десятками, а дюжинами, например, столовые приборы в сервизе или стулья в мебельном гарнитуре. Название единицы третьего разряда в двенадцатеричной системе — гросс — встречается теперь редко, но в торговой практике начала столетия оно еще бытовало.
Например, в написанном в 1928 стихотворении Плюшкин В.В.Маяковский, высмеивая людей, скупающих все подряд, писал: «…укупил двенадцать гроссов дирижерских палочек». У ряда африканских племен и в Древнем Китае была употребительна пятеричная система счисления.
В Центральной Америке (у древних ацтеков и майя) и среди населявших Западную Европу древних кельтов была распространена двадцатеричная система. Все они также связаны со счетом на пальцах.
Самой молодой системой счисления по праву можно считать двоичную. Эта система обладает рядом качеств, делающей ее очень выгодной для использования в вычислительных машинах и в современных компьютерах.
Позиционные и непозиционные системы счисления
Разнообразные системы счисления, которые существовали раньше и которые используются в наше время, можно разделить на непозиционные и позиционные. Знаки, используемые при записи чисел, называются цифрами.
В непозиционных системах счисления от положения цифры в записи числа не зависит величина, которую она обозначает. Примером непозиционной системы счисления является римская система, в которой в качестве цифр используются латинские буквы.
В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции. Количество используемых цифр называется основанием системы счисления.
Место каждой цифры в числе называется позицией. Первая известная нам система, основанная на позиционном принципе — шестидесятeричная вавилонская.
Цифры в ней были двух видов, одним из которых обозначались единицы, другим — десятки.
Однако наиболее употребительной оказалась индо-арабская десятичная система. Индийцы первыми использовали ноль для указания позиционной значимости величины в строке цифр. Эта система получила название десятичной, так как в ней десять цифр.
Различие между позиционой и непозиционной систем счисления легче всего понять на примере сравнения двух чисел. В позиционной системе счисления сравнение двух чисел происходит следующим образом: в рассматриваемых числах слева направо сравниваются цифры, стоящие в одинаковых позициях.
Бóльшая цифра соответствует бóльшему значению числа. Например, для чисел 123 и 234, 1 меньше 2, поэтому число 234 больше, чем число 123. В непозиционной системе счисления это правило не действует. Примером этого может служить сравнение двух чисел IX и VI.
Несмотря на то, что I меньше, чем V, число IX больше, чем число VI.
Позиционные системы счисления
Основание системы счисления, в которой записано число, обычно обозначается нижним индексом. Например, 5557 — число, записанное в семеричной системе счисления. Если число записано в десятичной системе, то основание, как правило, не указывается.
Основание системы — это тоже число, и его мы будем указывать в обычной десятичной системе. Вообще, число x может быть представлено в системе с основанием p, как x = an·pn +an — 1·pn–1 + a1·p1 + a0·p0, где an…
a0 – цифры в представлении данного числа. Так, например,
103510=1·103 + 0·102 + 3·101 + 5·100;
10102 = 1·23 + 0·22 + 1·21 + 0·20 = 10.
Наибольший интерес при работе на ЭВМ представляют системы счисления с основаниями 2, 8 и 16. Вообще говоря, этих систем счисления обычно хватает для полноценной работы как человека, так и вычислительной машины, однако иногда в силу различных обстоятельств все-таки приходится обращаться к другим системам счисления, например к троичной, семеричной или системе счисления по основанию 32.
Чтобы оперировать с числами, записанными в таких нетрадиционных системах, нужно иметь в виду, что принципиально они ничем не отличаются от привычной десятичной. Сложение, вычитание, умножение в них осуществляется по одной и той же схеме.
Почему же не используются другие системы счисления? В основном, потому, что в повседневной жизни люди привыкли пользоваться десятичной системой счисления, и не требуется никакая другая. В вычислительных же машинах используется двоичная система счисления, так как оперировать числами, записанными в двоичном виде, довольно просто.
Часто в информатике используют шестнадцатеричную систему, так как запись чисел в ней значительно короче записи чисел в двоичной системе.
Может возникнуть вопрос: почему бы не использовать для записи очень больших чисел систему счисления, например по основанию 50? Для такой системы счисления необходимы 10 обычных цифр плюс 40 знаков, которые соответствовали бы числам от 10 до 49 и вряд ли кому-нибудь понравится работать с этими сорока знаками. Поэтому в реальной жизни системы счисления по основанию, большему 16, практически не используются.
Перевод чисел из одной системы счисления в другую
Наиболее часто встречающиеся системы счисления — это двоичная, шестнадцатеричная и десятичная. Как же связаны между собой представления числа в различных системах счисления? Есть различные способы перевода чисел из одной системы счисления в другую на конкретных примерах.
Пусть нужно перевести число 567 из десятичной в двоичную систему. Сначала определяется максимальная степень двойки, такая, чтобы два в этой степени было меньше или равно исходному числу. В данном случае это 9, т.к. 29 =512, а 210 = 1024, что больше начального числа.
Таким образом получается число разрядов результата, оно равно 9 + 1 = 10, поэтому результат будет иметь вид 1ххххххххх, где вместо х могут стоять любые двоичные цифры. Вторая цифра результата находится так — двойка возводится в степень 9 и вычитается из исходного числа: 567 — 29 = 55. Остаток сравнивается с числом 28 = 256.
Так как 55 меньше 256, то девятый разряд — нуль, т.е. результат имеет вид 10хххххххх. Рассмотрим восьмой разряд. Так как 27 = 128> 55, то и он будет нулевым.
Седьмой разряд также оказывается нулевым. Искомая двоичная запись числа принимает вид 1000хххххх. 25 = 32 < 55, поэтому шестой разряд равен 1 (результат 10001ххххх). Для остатка 55 — 32 = 23 справедливо неравенство 24 = 16 < 23, что означает равенство единице пятого разряда. Аналогично получается в результате число 1000110111. Это число разлагается по степеням двойки:
567 = 1·29 + 0·28 + 0·27 + 0·26 + 1·25 + 1·24 + 0·23 + 1·22 + 1·21 + 1·20
При другом способе перевода чисел используется операция деления в столбик. Если взять то же число 567 и разделить его на 2, получается частное 283 и остаток 1. Та же операция производится и с числом 283. Частное — 141, остаток — 1.
Опять полученное частное делится на 2 и так до тех пор, пока частное не станет меньше делителя. Теперь, чтобы получить число в двоичной системе счисления, достаточно записать последнее частное, т.е.
1, и приписать к нему в обратном порядке все полученные в процессе деления остатки.
Результат, естественно, не изменился: 567 в двоичной системе счисления записывается как 1 000 110 111.
Эти два способа применимы при переводе числа из десятичной системы в систему с любым основанием. Например, при переводе числа 567 в систему счисления с основанием 16 число сначала разлагается по степеням основания. Искомое число состоит из трех цифр, т.к. 162 = 256
Второй способ состоит в последовательном делении в столбик, с единственным отличием в том, что делить надо не на 2, а на 16, и процесс деления заканчивается, когда частное становится строго меньше 16.
Конечно, для записи числа в шестнадцатеричной системе счисления, необходимо заменить 10 на A, 11 на B и так далее.
Операция перевода в десятичную систему выглядит гораздо проще, так как любое десятичное число можно представить в виде x = a0·pn + a1·pn–1 +… + an–1·p1 + an·p0, где a0 … an — это цифры данного числа в системе счисления с основанием p.
Например,так можно перевести число 4A3F в десятичную систему. По определению, 4A3F= 4·163 + A·162 + 3·16 + F. При замене A на 10, а F на 15, получается 4·163 + 10·162 + 3·16 + 15= 19007.
Проще всего переводить числа из двоичной системы в системы с основанием, равным степеням двойки (8 и 16), и наоборот.
Для того чтобы целое двоичное число записать в системе счисления с основанием 2n, нужно данное двоичное число разбить справа налево на группы по n-цифр в каждой; если в последней левой группе окажется меньше n разрядов, то дополнить ее нулями до нужного числа разрядов; рассмотреть каждую группу, как n-разрядное двоичное число, и заменить ее соответствующей цифрой в системе счисления с основанием 2n.
| Таблица 1. ДВОИЧНО-ШЕСТНАДЦАТЕРИЧНАЯ ТАБЛИЦА | ||||||||
| 2-ная | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 |
| 16-ная | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 2-ная | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
| 16-ная | 8 | 9 | A | B | C | D | E | F |
| Таблица 2. ДВОИЧНО-ВОСЬМЕРИЧНАЯ ТАБЛИЦА | ||||||||
| 2-ная | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| 8-ная | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Известный французский астроном, математик и физик Пьер Симон Лаплас (1749–1827) писал об историческом развитии систем счисления, что «Мысль выражать все числа девятью знаками, придавая им, кроме значения по форме, еще значение по месту, настолько проста, что именно из-за этой простоты трудно понять, насколько она удивительна. Как нелегко было прийти к этому методу, мы видим на примере величайших гениев греческой учености Архимеда и Аполлония, от которых эта мысль осталась скрытой.»
Сравнение десятичной системы исчисления с иными позиционными системами позволило математикам и инженерам-конструкторам раскрыть удивительные возможности современных недесятичных систем счисления, обеспечившие развитие компьютерной техники.
Анна Чугайнова
Источник: http://www.krugosvet.ru/node/41976
1.Для чего используются системы счисления? 2. Чем отличаются позиционные системы счисления от непозиционных? 3. Каково основание десятичной системы счисления, — презентация
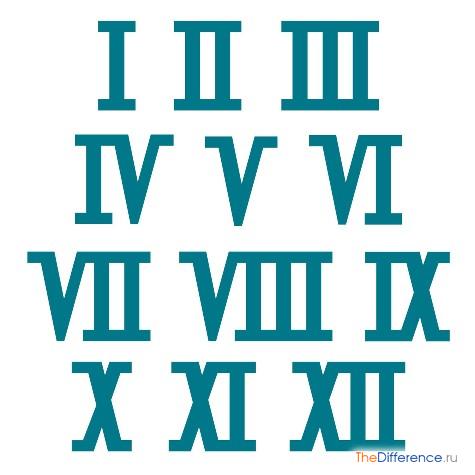
1<\p>
2 1. Для чего используются системы счисления? 2. Чем отличаются позиционные системы счисления от непозиционных? 3. Каково основание десятичной системы счисления, двоичной, восьмеричной и шестнадцатеричной? 4. Какие цифры входят в алфавит десятичной системы счисления, двоичной, восьмеричной и шестнадцатеричной? 5. Во сколько раз в позиционных системах счисления различаются одинаковые цифры, соседних разрядов числа? 7. Может ли в качестве цифры использоваться символ буквы? Назовите Римские цифры. Д/з<\p>
3 ВОПРОВЫ ТЕСТА: Какие цифры входят в алфавит восьмеричной системы счисления Какие числа записаны римскими цифрами: МСХIХ За единицу количества информации принимается: Какие цифры входят в алфавит двоичной системы счисления Укажите самое большое число: , , 100 2, Двоичное число соответствует десятичному числу Чем отличаются позиционные системы счисления от непозиционных? Для чего используются системы счисления может ли число 48А1 записано в системе счисления десятичной, восьмеричной, шестнадцатеричной Где правильно записаны числа в соответствующих системах счисления: 1А0В 16, , , , Д/з<\p>
4 Какие числа записаны римскими цифрами: а) MCMXCIX; б) CMLXXXVIII; в) MCXLVII?MCMXCIXCMLXXXVIIIMCXLVII? Запишите в развернутой форме числа: А 8 = ; А 2 =101001; А 16 = ; А 8 = А 2 =101001А 16 = А 10 = 143,511; А 8 =0,134512;А 10 = 143,511А 8 =0, А 16 = 1В3,5С2. Д/з<\p>
5 Двоичная система счисления является стандартом при конструировании компьютеров, т.к. наиболее просто технически создать электронные схемы, работающие в двух устойчивых состояниях (0 и 1); просто выполняются арифметические действия; для выполнения логических операций можно применить алгебру логики. Двоичная СС используется для организации машинных операций по преобразованию информации, десятичная — для ввода и вывода информации, восьмеричная и шестнадцатеричная — для составления программ на языке машинных кодов для более короткой и удобной записи двоичных кодов.<\p>
6 Арифметические операции во всех позиционных СС выполняются по одним и тем же правилам. Важно помнить алфавит СС: 2-я — 0, 1; 8-я — 0 — 7; 16-я — 0 — 9, A — F. При переполнении разряда, когда величина числа становится равной или большей основания, производится перенос в старший разряд при сложении и заём из старшего разряда при вычитании. Величина переноса в следующий разряд при сложении и заём из старшего разряда при вычитании определяется величиной основания системы счисления: в 2-й СС — основанием 2, в 8-й — 8, в 16-й — 16.<\p>
7 При выполнении арифметических операций можно пользоваться таблицей представления чисел в различных СС. Представление чисел в различных системах счисления. N 10 N2N2 N8N8 N A (10) B (11) C (12) D (13) E (14) F (15)<\p>
8 0 + 0= = = = 10 Арифметические операции во всех позиционных системах счисления выполняются по одним и тем же хорошо известным вам правилам. Двоичная система счисления. Сложение.Сложение. В его основе лежит таблица сложения одноразрядных двоичных чисел:<\p>
9 Проверим правильность вычислений сложением в десятичной системе счисления.<\p>
10 Вычитание. Двоичная система счисления. В его основе лежит таблица вычитания одноразрядных двоичных чисел. При вычитании из меньшего числа (0) большего (1) производится заем из старшего разряда. В таблице заем обозначен 1 с чертой:<\p>
11 Умножение. Двоичная система счисления. В основе умножения лежит таблица умножения одноразрядных двоичных чисел: 0 * 0 = 0 0 * 1 = 0 1 * 0 = 0 1 * 1 = 1<\p>
12 Деление. Двоичная система счисления. Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления.<\p>
13 Для проведения операций над числами, выраженными в различных системах счисления, необходимо предварительно перевести их в одну и ту же систему. Д/з<\p>
14 . Числа и 10 2 : а) сложить; б) вычесть; в) умножить; г) разделить ; Д/з<\p>
15 . Числа и 10 2 : а) сложить (1100); б) вычесть (1000); в) умножить (10100); г) разделить (101) ; Д/з<\p>
16<\p>
17 Вариант 1 Вычислить: = = = = Вариант 2 Вычислить: = = = =<\p>
18 3. Запишите в развернутом виде числа: Д/з<\p>
19 I=10 X=10 C=100 M=1000 V=5 L=50 D=500<\p>
20 ( )+ ( )+(10-1) 1999 MCMXCIX<\p>
21 ( ) I=10 X=10 C=100 M=1000 V=5 L=50 D=500 CMLXXXVIII<\p>
22 (50-10) I=10 X=10 C=100 M=1000 V=5 L=50 D=500 MCXLVII<\p>
23 А 8 =<\p>
24 А 2 =101001<\p>
25 А 16 = 15361<\p>
26 А 10 = 143,511=<\p>
27 А 8 =0,134512=<\p>
28 А 16 = 1В3,5С2=<\p>
29 1. Правильно ли записаны числа в соответствующих системах счисления: а) б); в) д) 2. Запишите в свернутой форме следующие числа: а) б)<\p>
30 Д/з: § Задания для самостоятельного выполнения 3.1 — 3.6<\p>
31 1. Числа 41 8 и 17 8 : а) сложить; б) вычесть ; Умножить 46 8 и 2 8 Разделить 52 8 и 2 8. Сложить числа и 9 16 Вычесть числа 5В 16 и 6 16 Умножить числа и 2 16 Разделить числа 2Е 16 и 2 16 Сложить числа 10 2 и А 16<\p>
32 1. Числа 41 8 и 17 8 : а) сложить (60); б) вычесть (22); Умножить 46 8 и 2 8 (114). Разделить 52 8 и 2 8 (25). Сложить числа и 9 16 (4А). Вычесть числа 5В 16 и 6 16 (55). Умножить числа и 2 16 (8А). Разделить числа 2Е 16 и 2 16 (17). Сложить числа 10 2 и А 16 ( =12 10 ).<\p>
Источник: http://www.myshared.ru/slide/1373249/




