Разница между волной и колебаниями

Волны и колебания — обычные явления в окружающем мире. Рассмотрим, что они собой представляют и чем отличается волна от колебаний.
Определение
Волна — возмущение, возникшее в какой-либо среде и распространяющееся в ней со временем.
Волны на воде
Колебания — движения возвратно-поступательного характера, совершаемые некоторым телом или частицами.
Колебания
Сравнение
И в том и в другом случае происходит процесс перемещения. Но отличие волны от колебаний заключается в характере такого движения.
Волне свойственно распространение на определенное расстояние относительно места ее возникновения. При этом наблюдается чередование максимальных и минимальных параметров (например, плотности или температуры).
В геометрическом изображении такого явления присутствуют гребни и понижения.
Волна может возникать в разных средах. Ее легко увидеть, например, бросив в воду тяжелый предмет. В толще земли действуют сейсмические волны, в воздухе — световые. Характерным свойством подобных возмущений, какова бы ни была их природа, является перемещение энергии из одной зоны в другую. Вещество же при этом, как правило, не переносится, хотя такой вариант не исключен.
Тем временем при колебаниях отсутствует протяженное перемещение энергии. Здесь происходит переход последней то в одну, то в другую форму.
Сам процесс осуществляется в ограниченном пространстве и характеризуется периодически повторяющимся изменением того состояния системы, которое она принимает относительно точки равновесия.
При механических колебаниях наблюдается перемещение вещества (маятник, качели, груз на пружине). При электромагнитных — передвигаются только частицы. В последнем случае примером будет процесс, происходящий в колебательном контуре.
Стоит отметить, что обсуждаемые явления не рассматриваются полностью изолированными друг от друга. Волну можно образно представить как «растянутое» колебание, в котором, при чередовании фаз, действует уже не одна материальная точка, а множество таких взаимосвязанных элементов.
Лучше понять, в чем разница между волной и колебаниями, поможет и следующий пример. Представим, что тело в механической системе под действием силы выводится из равновесия.
Возникает движение объекта с постоянной сменой направления, или колебание. В процесс вовлекается окружающая среда. Вещество в ней начинает сжиматься и разряжаться.
Возмущение распространяется с определенной скоростью все дальше от источника. Такой процесс уже является волновым.
Источник: https://TheDifference.ru/raznica-mezhdu-volnoj-i-kolebaniyami/
Почему нельзя считать колебания маятника волной?

Волна — возмущение состояния среды (изменение), которое распространяется в данной среде, перенося с собой энергию.
Иначе говоря, пространственное чередование максимумов и минимумов любой пространственной величины (температура, плотность, напряженность электрического поля и т.д.), которое изменяется со временем, и есть волна.
Более верным определением волны будет следующим: Волна — есть явление распространения в пространстве с течением времени возмущения физической величины.
Вне зависимости от природы волны осуществление переноса энергии происходит без переноса вещества. Перенос вещества может произойти только в роли побочного эффекта.
Процесс , в котором имеют место быть только ”местные” преобразования энергии, является принципиальным отличием волны от колебания. Волны обычно имеют способность отдаляться на порядочные расстояния относительно места, в котором они возникли.
В следствие этого волнам иногда дают такое название, как ”колебание, оторвавшееся от излучателя”.
Маятником называют твердое тело, которое под действием приложенных сил совершает колебания возле неподвижной точки либо оси. В физике в основном имеют понятие маятника, как тела, совершающего колебания под действием силы тяжести, ось которого не проходит через центр тяжести данного тела.
Самым простым маятником является небольшой массивный груз С, который подвешен на нити, имеющей длину l.
Если условиться, что данная нить нерастяжима, и проигнорировать размерами груза в сравнении с длиной нити, а так же массой нити в сравнении с массой груза, то груз, подвешенный на данную нить можно рассматривать как материальную точку, которая находится на неизменном расстоянии l от точки подвеса О.
Данный маятник носит название математического маятника. Принимая во внимание вышеперечисленные условия, можно ответить на вопрос, почему колебания математического маятника нельзя считать волной? В случае, когда колеблющееся тело нельзя рассмотреть как материальную точку, маятник будет называться физическим.
✔ Открой Секрет ➔ Почему нельзя заряжать телефон ночью?
Большая часть волн по своей сущности новыми физическими явлениями не являются, если только условным названием для определенного вида коллективного движения.
Если в объеме газа появилась звуковая волна, то это вовсе не означает, что в данном объеме возникли некие новые физические объекты. Звуком называют лишь особый скоординированный тип перемещения тех же самых молекул.
По-другому говоря, большая часть волн — это колебания некоторой среды. За рамками данной среды волны этого типа не существуют (к примеру, звук в вакууме).
Несмотря на это, существуют волны, не являющиеся ”зыбью” какой либо другой среды, а являются непосредственно новыми физическими явлениями.
Например, электромагнитные волны в современной физике называют не колебание какой-либо среды (имела название ”эфир” в XIX веке), а самостоятельное поле, способное самоподдерживаться, которое имеет свойство распространяться в вакууме. Так же происходит и с волнами вероятности материальных частиц.
✔ Открой Секрет ➔ Почему нельзя скачать экспонат в айтюнс?
Волнами называют также и некоторые явления, но каждая из этих волн имеет свою индивидуальную специфику. К примеру, так иногда говорят о волнах горения, волнах плотности реагентов, волнах химических реакций, волнах плотности транспортных потоков, температурных волнах, волнах вероятности электрона и иных частиц.
Стоит уделить внимание тому, что явления, которые выглядят как волны, но которые не способны к самораспространению, не являются волнами (к примеру, песчаные дюны).
Источник: https://pochemy-nelzya.info/schitat-kolebaniya-mayatnika-volnoj/
Механические колебания и волны Колебания и волны

Механические колебания и волны
Колебания и волны • Колебания — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия.
– Например, при колебаниях маятника повторяются отклонения его в ту и другую сторону от вертикального положения; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку.
• Колебания почти всегда связаны с попеременным превращением энергии одной формы проявления в другую форму. • Колебания различной физической природы имеют много общих закономерностей и тесно взаимосвязаны c волнами.
Поэтому исследованиями этих закономерностей занимается обобщённая теория колебаний и волн. Принципиальное отличие от волн: при колебаниях не происходит переноса энергии, это, так сказать, «местные» преобразования энергии.
Классификация ПО ФИЗИЧЕСКОЙ ПРИРОДЕ • Механические (звук, вибрация) • Электромагнитные (свет, радиоволны, тепловые) • Смешанного типа — комбинации вышеперечисленных
Классификация ПО ХАРАКТЕРУ ВЗАИМОДЕЙСТВИЯ С ОКРУЖАЮЩЕЙ СРЕДОЙ Вынужденные — колебания, протекающие в системе под влиянием внешнего периодического воздействия. Примеры: листья на деревьях, поднятие и опускание руки.
При вынужденных колебаниях может возникнуть явление резонанса: резкое возрастание амплитуды колебаний при совпадении собственной частоты осциллятора и частоты внешнего воздействия.
Свободные (или собственные) — это колебания в системе под действием внутренних сил, после того как система выведена из состояния равновесия (в реальных условиях свободные колебания всегда затухающие). Простейшими примерами свободных колебаний являются колебания груза, прикреплённого к пружине, или груза, подвешенного на нити.
Классификация ПО ХАРАКТЕРУ ВЗАИМОДЕЙСТВИЯ С ОКРУЖАЮЩЕЙ СРЕДОЙ Автоколебания — колебания, при которых система имеет запас потенциальной энергии, расходующейся на совершение колебаний (пример такой системы — механические часы).
Характерным отличием автоколебаний от свободных колебаний является, то что их амплитуда определяется свойствами самой системы, а не начальными условиями. Параметрические — колебания, возникающие при изменении какого-либо параметра колебательной системы в результате внешнего воздействия.
Случайные — колебания, при которых внешняя или параметрическая нагрузка является случайным процессом.
Классификация Гармонические колебания — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону.
Механические колебания Наряду с поступательными и вращательными движениями тел в механике значительный интерес представляют и колебательные движения.
Механическими колебаниями называют движения тел, повторяющиеся точно (или приблизительно) через одинаковые промежутки времени. Закон движения тела, совершающего колебания, задается с помощью некоторой периодической функции времени x = f (t).
Графическое изображение этой функции дает наглядное представление о протекании колебательного процесса во времени.
Механические колебания Примерами простых колебательных систем могут служить груз на пружине или математический маятник (рис. 1). Рисунок 1. Механические колебательные системы
Характеристики механических колебаний Амплитуда — максимальное отклонение колеблющейся величины от некоторого усреднённого её значения для системы, A или xm (м) Период — промежуток времени, через который повторяются какие-либо показатели состояния системы (система совершает одно полное колебание), Т (с) Частота — число колебаний в единицу времени, f (Гц, с− 1). Период колебаний и частота — обратные величины: В круговых или циклических процессах вместо характеристики «частота» используется понятие круговая (циклическая) частота ω (рад/с, с− 1), показывающая число колебаний за 2π единиц времени.
Характеристики механических колебаний Смещение — отклонение тела от положения равновесия. Обозначение Х, Единица измерения метр. Фаза колебаний — определяет смещение в любой момент времени, то есть определяет состояние колебательной системы.
Механические колебания • Простейшим видом колебательного процесса являются простые гармонические колебания, которые описываются уравнением x = xm cos (ωt + φ0). • Здесь x — смещение тела от положения равновесия, xm — амплитуда колебаний, т. е.
максимальное смещение от положения равновесия, ω — циклическая или круговая частота колебаний, t — время. Величина, стоящая под знаком косинуса φ = ωt + φ0 называется фазой гармонического процесса.
При t = 0 φ = φ0, поэтому φ0 называют начальной фазой.
Механические колебания • Рис. 2. иллюстрирует изменения, которые происходят на графике гармонического процесса, если изменяются либо амплитуда колебаний xm, либо период T (или частота f), либо начальная фаза φ0. • Рисунок 2.
Во всех трех случаях для синих кривых φ0 = 0: • а — красная кривая отличается от синей только большей амплитудой (x'm> xm); b — красная кривая отличается от синей только значением периода (T' = T / 2); с — красная кривая отличается от синей только значением начальной фазы.
Свободные колебания. Пружинный маятник • Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.
• Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению: F (t) = ma (t) = –m ω2 x (t).
Свободные колебания. Пружинный маятник • В этом соотношении ω — круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука: Fупр = –kx.
• Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими. • Таким образом, груз некоторой массы m, прикрепленный к пружине жесткости k, второй конец которой закреплен неподвижно (рис.
), составляют систему, способную в отсутствие трения совершать свободные гармонические колебания. Груз на пружине называют линейным гармоническим осциллятором.
Свободные колебания. Пружинный маятник • Круговая частота ω0 свободных колебаний груза на пружине находится из второго закона Ньютона: откуда • Частота ω0 называется собственной частотой колебательной системы. • Период T гармонических колебаний груза на пружине равен
Свободные колебания. Математический маятник • Математическим маятником называют тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела.
В положении равновесия, когда маятник висит по отвесу, сила тяжести уравновешивается силой натяжения нити. При отклонении маятника из положения равновесия на некоторый угол φ появляется касательная составляющая силы тяжести Fτ = –mg sin φ (рис. ).
Знак «минус» в этой формуле означает, что касательная составляющая направлена в сторону, противоположную отклонению маятника.
Свободные колебания. Математический маятник • Только в случае малых колебаний математический маятник является гармоническим осциллятором, т. е. системой, способной совершать гармонические колебания. Практически такое приближение справедливо для углов порядка 15– 20°; при этом. • Колебания маятника при больших амплитудах не являются гармоническими.
Свободные колебания. Математический маятник • Формула выражает собственную частоту малых колебаний математического маятника. Тогда период: l — длина нити, g — ускорение свободного падения
Превращения энергии при свободных механических колебаниях При свободных механических колебаниях кинетическая и потенциальная энергии изменяются периодически.
При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения.
Для груза на горизонтально расположенной пружине потенциальная энергия — это энергия упругих деформаций пружины. Для математического маятника — это энергия в поле тяготения Земли.
Превращения энергии при свободных механических колебаниях • Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией.
• Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д.
• Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот.
Превращения энергии при свободных механических колебаниях Рис. 4. Превращения энергии при свободных колебаниях
Превращения энергии при свободных механических колебаниях • В реальных условиях любая колебательная система находится под воздействием сил трения (сопротивления). При этом часть механической энергии превращается во внутреннюю энергию теплового движения атомов и молекул, и колебания становятся затухающими Рис. 4. Затухающие колебания
Вынужденные колебания. Резонанс. Автоколебания • Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными. • В этом случае внешняя сила совершает положительную работу и обеспечивает приток энергии к колебательной системе.
Она приток энергии не дает колебаниям затухать, несмотря на действие сил трения. • Периодическая внешняя сила может изменяться во времени по различным законам.
Особый интерес представляет случай, когда внешняя сила, изменяющаяся по гармоническому закону с частотой ω, воздействует на колебательную систему, способную совершать собственные колебания на некоторой частоте ω0.
• Если свободные колебания происходят на частоте ω0, которая определяется параметрами системы, то установившиеся вынужденные колебания всегда происходят на частоте ω внешней силы.
Вынужденные колебания. Резонанс. Автоколебания • После начала воздействия внешней силы на колебательную систему необходимо некоторое время Δt для установления вынужденных колебаний Время установления по порядку величины равно времени затухания τ свободных колебаний в колебательной системе.
• В начальный момент в колебательной системе возбуждаются оба процесса — вынужденные колебания на частоте ω и свободные колебания на собственной частотеω0. Но свободные колебания затухают из-за неизбежного наличия сил трения.
Поэтому через некоторое время в колебательной системе остаются только стационарные колебания на частоте ω внешней вынуждающей силы.
Вынужденные колебания. Резонанс. Автоколебания • Если частота ω внешней силы приближается к собственной частоте ω0, возникает резкое возрастание амплитуды вынужденных колебаний. Это явление называется резонансом.
Зависимость амплитуды xm вынужденных колебаний от частоты ω вынуждающей силы называется резонансной характеристикой илирезонансной кривой (рис. 5). Рисунок 5.
Резонансные кривые при различных уровнях затухания: 1 — колебательная системабез трения; при резонансе амплитуда xm вынужденных колебаний неограниченно возрастает; 2, 3, 4 — реальные резонансные кривые для колебательных систем с различной силой трения
Вынужденные колебания. Резонанс. Автоколебания • При резонансе амплитуда xm колебания груза может во резонансе много раз превосходить амплитуду ym колебаний свободного (левого) конца пружины, вызванного внешним воздействием.
• В отсутствие трения амплитуда вынужденных колебаний при резонансе должна неограниченно возрастать.
• В реальных условиях амплитуда установившихся вынужденных колебаний определяется условием: работа внешней силы в течение периода колебаний должна равняться потерям механической энергии за то же время из-за трения. Чем меньше трение, тем больше амплитуда вынужденных колебаний при резонансе.
Вынужденные колебания. Резонанс. Автоколебания • Вынужденные колебания — это незатухающие колебания. Неизбежные потери энергии на трение компенсируются подводом энергии от внешнего источника периодически действующей силы.
Существуют системы, в которых незатухающие колебания возникают не за счет периодического внешнего воздействия, а в результате имеющейся у таких систем способности самой регулировать поступление энергии от постоянного источника.
• Такие системы называются автоколебательными, а процесс незатухающих колебаний в таких системах — автоколебаниями. В автоколебательной системе можно выделить три характерных элемента — колебательная система, источник энергии и устройство обратной связи между колебательной системой и источником.
В качестве колебательной системы может быть использована любая механическая система, способная совершать собственные затухающие колебания (например, маятник настенных часов)
Механические волны • Если в каком-нибудь месте твердой, жидкой или газообразной среды возбуждены колебания частиц, то вследствие взаимодействия атомов и молекул среды колебания начинают передаваться от одной точки к другой с конечной скоростью.
Процесс распространения колебаний в среде называется волной. • Механические волны бывают разных видов. • Если в волне частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, то волна называется поперечной.
Примером волны такого рода могут служить волны, бегущие по натянутому резиновому жгуту (рис. ) или по струне.
Механические волны • Если смещение частиц среды происходит в направлении распространения волны, то волна называется продольной. Волны в упругом стержне (рис. ) или звуковые волны в газе являются примерами таких волн. • Волны на поверхности жидкости имеют как поперечную, так и продольную компоненты.
• Как в поперечных, так и в продольных волнах переноса вещества в направлении распространения волны не происходит. В процессе распространения частицы среды лишь происходит совершают колебания около положений равновесия.
Однако волны переносят энергию колебаний от одной точки среды к волны переносят энергию другой.
Механические волны • Характерной особенностью механических волн является то, что они распространяются в материальных средах (твердых, жидких или газообразных). Существуют волны, которые способны распространяться и в пустоте (например, световые волны).
• Для механических волн обязательно нужна среда, обладающая обязательно нужна среда способностью запасать кинетическую и потенциальную энергию. Следовательно, среда должна обладать инертными и упругими свойствами. В реальных средах эти свойства распределены по свойствами всему объему. • Так, например, любой малый элемент твердого тела обладает массой и упругостью.
В простейшей одномерной модели твердое тело можно представить как совокупность модели шариков и пружинок (рис. ). • Простейшая одномерная модель твердого тела
Механические волны • В этой модели инертные и упругие свойства разделены. Шарики обладают массой m, а пружинки — жесткостью k. С помощью такой простой модели можно описать распространение продольных и поперечных волн в твердом теле.
• В продольных волнах шарики испытывают смещения вдоль цепочки, а пружинки растягиваются или сжимаются. Такая деформация называется деформацией растяжения или сжатия. В жидкостях или газах деформация такого рода сопровождается уплотнением или разрежением.
• Продольные механические волны могут распространяться в любых средах — твердых, жидких и газообразных.
Механические волны • Если в одномерной модели твердого тела один или несколько шариков сместить в направлении, перпендикулярном цепочке, то возникнет деформация сдвига. Деформированные при таком смещении пружины будут стремиться возвратить смещенные частицы в положение равновесия.
При этом на ближайшие несмещенные частицы будут действовать упругие силы, стремящиеся отклонить их от положения равновесия. В результате вдоль цепочки побежит поперечная волна.
• В жидкостях и газах упругая деформация сдвига не возникает Если один слой жидкости или газа сместить на некоторое расстояние относительно соседнего слоя, то никаких касательных сил на границе между слоями не появится.
Силы, действующие на границе жидкости и твердого тела, а также силы между соседними слоями жидкости всегда направлены по нормали к границе — это силы давления. То же относится к газообразной среде. • Следовательно, поперечные волны не могут существовать в жидкой или газообразной средах.
Механические волны • Значительный интерес для практики представляют простые гармонические или синусоидальные волны. Они характеризуются амплитудой A колебания частиц, частотой f и длиной волны λ. Синусоидальные волны распространяются в однородных средах с некоторой постоянной скоростью υ. • «Моментальные фотографии» бегущей синусоидальной волны в момент времени t + Δt
Источник: http://present5.com/mexanicheskie-kolebaniya-i-volny-kolebaniya-i-volny/
Колебания и волны
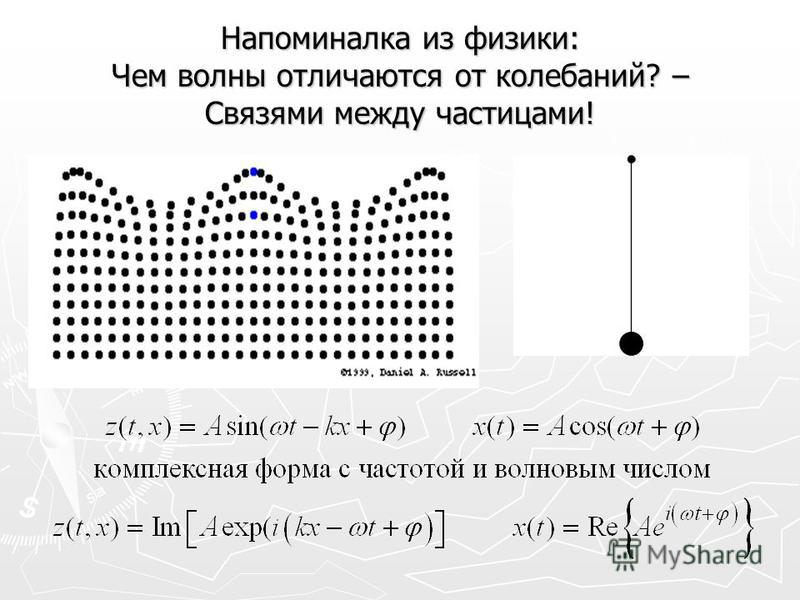
Колебания — повторяющийся в той или иной степени во времени процесс изменения состояний системы. Например, при колебаниях маятника повторяются отклонения его в ту и другую сторону от вертикального положения; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку.
Колебания почти всегда связаны с попеременным превращением энергии одной формы проявления в другую форму.
Отличие колебания от волны.
Колебания различной физической природы имеют много общих закономерностей и тесно взаимосвязаны c волнами. Поэтому исследованиями этих закономерностей занимается обобщённая теория колебаний и волн. Принципиальное отличие от волн: при колебаниях не происходит переноса энергии, это, так сказать, «местные» преобразования энергии.
Классификации колебаний
Выделение разных видов колебаний зависит от свойства, которое хотят подчеркнуть.
Для подчёркивания разной физической природы колеблющихся систем (осцилляторов) выделяют, например, колебания:
- механические (звук, вибрация);
- электромагнитные (свет, радиоволны, тепловые);
- комбинации вышеперечисленных;
По характеру взаимодействия с окружающей средой:
- вынужденные — колебания, протекающие в системе под влиянием внешнего периодического воздействия;
- собственные или свободные — колебания при отсутствии внешних сил, когда система, после первоначального воздействия внешней силы, предоставляется самой себе (в реальных условиях свободные колебания всегда затухающие);
- автоколебания — колебания, при которых система имеет запас потенциальной энергии и она расходуется на совершение колебаний (пример такой системы — механические часы).
Характеристики колебаний
Амплитуда(м) — максимальное отклонение колеблющейся величины от некоторого усреднённого её значения для системы.
Промежуток времени(сек), через который повторяются какие-либо показатели состояния системы (система совершает одно полное колебание), называют периодом колебаний.
Число колебаний в единицу времени называется частотой колебаний(Гц, сек-1).
Период колебанийи частота– обратные величины;
и
В круговых или циклических процессах вместо характеристики «частота» используется понятие круговая или циклическая частота(Гц, сек-1, об/сек), показывающая число колебаний за время 2π:
Фаза колебаний — определяет смещение в любой момент времени, т.е. определяет состояние колебательной системы.
| Меркурий
Меркурий — ближайшая к Солнцу планета. Древние римляне считали Меркурия покровителем торговли, путешественников и воров, а также вестником богов. Неудивительно, что небольшая планета, быстро перемещающаяся по небу вслед за Солнцем, получила его имя. Меркурий был известен еще с древних времен, однако древние астрономы не сразу поняли, что утром и вечером … |
Измерение времени
Ответить на вопрос «что такое время» нелегко. В самом общем виде можно сказать, что время — это непрерывная череда сменяющих друг друга явлений. Главное свойство времени состоит в том, что оно длится, течет безостановочно. Пространство можно оградить, но время остановить невозможно. Время необратимо — путешествия на машине времени в прошлое невозможны. «Нельзя … |
| Слог + картинка
Слог + картинка На этапе самостоятельного чтения используется упражнение “Слог + картинка”. Такого рода задания редко встречаются в учебных пособиях, но они очень полезны, так как способствуют раннему формированию осмысленного чтения. Ребенку предлагается соединить картинку со слогом, на который начинается ее название. В другом варианте задания под … |
Патрокл — заблудившаяся комета
|
Источник: http://for-schoolboy.ru/Kolebaniya-i-volnyi-937.html




