Как на самом деле строились Египетские пирамиды?
Древние египтяне не знали ни стали, ни подъемных кранов, а пирамиду для фараона надо было строить. Как они справились с задачей, ученые поняли только сейчас.
Египтяне считали фараона богом, и возведение роскошной гробницы для него обеспечивало, по их мнению, покровительство высших сил всей стране. Великая пирамида фараона Хуфу (по-гречески — Хеопса), рекордсменка среди древнеегипетских пирамид, изначально была 146,7 метра высотой — с современный небоскреб этажей в 48.
После того как верхний камень, пирамидион, и несколько блоков кладки рухнули (вероятно, из-за землетрясения), сооружение стало почти на девять метров ниже. Цивилизации сменяли друг друга, но пирамида Хуфу оставалась самым высоким зданием в мире без малого четыре тысячелетия (пока в Англии в 1311 году не построили линкольнский собор Девы Марии высотой 160 метров).
А площадь ее основания такова, что там вполне уместились бы шесть-семь футбольных полей.Пирамиду Хуфу построили в XXVI веке до н. э., это самая древняя из гробниц фараонов на плато Гиза. Трудно поверить, но люди, возводившие Великую пирамиду, не использовали железных инструментов, не говоря уже о стальных.
Они знали только медь, дерево и камень и примитивные устройства, не сложнее колодезного журавля. Мистики вообще отказываются верить, что возвести такую грандиозную конструкцию под силу человеку медно-каменного века без содействия, скажем, инопланетян с антигравитационными приспособлениями.
Ученые к концу XX столетия многое узнали о людях, которые строили пирамиду Хуфу, но поиски правдоподобного объяснения, с помощью каких инженерных решений древним египтянам это удалось, продолжались…
Материал
Известняк и гранитЧтобы огромная пирамида была устойчивой, известняковые блоки, из которых она сложена, должны быть массивными. Колесный транспорт для перевозки камней не использовали — технологии того времени не позволяли делать достаточно прочные оси и ободы, чтобы колеса выдержали такой груз. Воображение рисует страшную картину, как десятки человек волоком тащат эти глыбы на стройку за многие километры от места выработки. Но все не так уж страшно, если место для Великой пирамиды выбрано правильно. Архитекторы расположили ее вплотную к карьеру, где добывали серо-желтый известняк, из которого сделана основная часть сооружения. С другой стороны, недалеко был Нил, главная транспортная артерия Древнего Египта, и прочие виды камня можно было доставлять по воде. Для строительных нужд на реке соорудили гавань.Серо-желтый известняк — материал достаточно рыхлый и сравнительно легко поддается обработке. Глыбы вырубали из породы медными кирками, пилами и каменными молотами и шлифовали булыжниками прямо в карьере. Затем отряды грузчиков доставляли их на стройку. Камень ставили на сани-волокуши из кедровых стволов и тащили за веревки. На древнеегипетском изображении под полозья льют жидкость, видимо масло или воду, чтобы облегчить скольжение.В наши дни кладка серо-желтого известняка хорошо видна, но в древности пирамида Хуфу выглядела совсем по-другому. Ее стены были светло-бежевыми, гладкими и сверкали на солнце благодаря облицовке, к сожалению, утраченной в Средневековье. Блоки облицовки, эту «одежду» пирамиды, делали из более прочной и красивой разновидности известняка светлого, почти белого цвета. Его добывали в карьерах Туры — в 13 километрах вверх по течению Нила на противоположном его берегу. Камни полировали до блеска и тщательно подгоняли друг к другу по форме.
Гранитные плиты для отделки внутренних камер везли по Нилу за 800 километров из Асуана.
Глыбы этого ценного минерала, слишком твердого для медных инструментов, вырубали из скал с помощью деревянных клиньев: их вставляли в трещину и поливали водой, дерево разбухало, и трещина увеличивалась.Главная тайна: подъем тяжестей
Версия
Внешний пандус
Сооружать внешний пандус с необходимым углом наклона (7–8 градусов) до самой вершины — дело слишком затратное.В основании пирамиды Хуфу — цельный скальный массив. Рабочие обтесали его и обложили блоками по периметру, что сэкономило ресурсы и придало строению устойчивости. Первые ряды камней заложены. Известняковые, а постепенно и гранитные глыбы планомерно доставлялись на строительство, сооружение росло… И тут мы сталкиваемся с главной загадкой Великой пирамиды: как древние зодчие поднимали несметное количество тяжелых камней наверх, все выше и выше?
Размер известняковых блоков, из которых сложена основная часть пирамиды, от основания к вершине все меньше, но средняя их высота — около 90 см, а масса кубометра этого материала — около двух тонн.
Древнегреческий историк Геродот через две тысячи лет после возведения пирамиды Хуфу писал, что на строительстве применяли некие подъемные приспособления из деревянных балок.
Египтяне знали простейшие конструкции, основанные на принципе рычага, но если бы пирамиду возводили только с их помощью, таких балок понадобилось бы слишком много для небогатого лесом Египта. Постепенно ученые пришли к выводу, что камни можно было затащить наверх только по наклонному пандусу.
Но теория о большой пологой насыпи с одной стороны постройки тоже оказалась уязвимой: пандус с необходимым углом наклона простирался бы на полтора километра от пирамиды и потребовал бы стольких же затрат, сколько на нее саму.
В случае, если внешняя насыпь равномерно наращивалась со всех сторон, было бы невозможно контролировать нужный угол наклона граней возводимой пирамиды. Очевидное и вроде бы простое решение стало казаться неубедительным.
Процесс
Все выше и выше
«Кухня» строительства Великой пирамиды
1 Пирамидион — глыбу пирамидальной формы массой около 15 т — возможно, доставили по пандусу заранее и поднимали до вершины по мере сооружения верхних ярусов. Он, вероятно, был покрыт сплавом золота и серебра.
2 На углах, где пандус поворачивал на 90 градусов, древние строители оставляли площадку, чтобы силами нескольких рабочих можно было разворачивать массивные каменные плиты, которые они втаскивали наверх. Пустоты, обозначающие такие площадки, обнаружены археологами на гранях пирамиды.
3 Каменные блоки доставляли с южной стороны пирамиды, к которой были ближе карьер и гавань.Возможно, рабочие использовали деревянный подъемный механизм, основанный на противовесе, чтобы облегчать перемещение грузов на самых трудных участках и на строительстве верхних ярусов.Длина стороны основания пирамиды Хуфу примерно 230 м.
Площадь основания — 5,3 га.Основная часть пирамиды была сложена из 210 рядов блоков. До наших дней сохранился 201 ряд.Блоки клали рядами горизонтально, а не под углом к земной поверхности, в отличие от самой древней пирамиды фараона Джосера.
Устойчивая конструкция из горизонтально положенных камней требовала более тщательных расчетов и качественной шлифовки камня, но такой способ позволял построить пирамиду гораздо выше и массивнее.Новые версии: спиральный серпантинОчередную теорию о наклонной насыпи на рубеже XXI века выдвинул французский архитектор Жан-Пьер Уден.
Она одной, но принципиальной деталью отличалась от предыдущих. По его мнению, невысокий внешний пандус служил для возведения нижних ярусов и подъема наиболее тяжелых плит для верхних камер. Камни для дальнейшего строительства тоже доставляли по пандусу, но не внешнему, а внутреннему, являвшемуся частью постройки.
Выкладывая блоки ярус за ярусом, египтяне параллельно обустраивали в пирамиде, вдоль ее наружных поверхностей, крытую галерею, ведущую наверх по спирали. По наклонной насыпи внутри нее волоком тащили блоки для новых ярусов.
Интерьер
Прогулочные шахтыПирамида Хуфу скрывает в себе не только усыпальницу фараонаПять «разгрузочных камер» из гранита сделаны, чтобы потолок камеры не рухнул под тяжестью блоков.В «камере фараона» находится гранитный саркофаг. Тело царя, вероятно, похищено из него в древности.Название «камера царицы» условно: жен фараонов хоронили в отдельных малых пирамидах при царской. Возможно, она построена в качестве «предварительной» усыпальницы фараона до сооружения верхней камеры.Нисходящий лаз, по мнению исследователей, предназначен для стока вод с верхних ярусов.«Вентиляционные шахты» могли служить для доступа воздуха, но есть гипотеза, что, по мысли египтян, душа царя через них покидала камеру.Строители пирамид почти всегда располагали вход на севере: вероятно, из религиозных соображений.Большая галерея выложена из гранита. Такой конструкции нет ни в одной другой пирамиде.Подземная камера прорублена в скале, лежащей в основании пирамиды.Еще в конце 1980-х годов пирамиду Хуфу исследовали методом микрогравиметрии, в основе которого лежит измерение силы тяжести, и в результате выявили внутри строения участки меньшей плотности. Такие участки складываются в спиральную структуру, что подтверждает гипотезу УденаОрехов Р.А. Мир строителей пирамид. Эпоха Древнего царства. СПб.: «Контраст», 2014Российский египтолог Роман Орехов возразил, что сооружение крытой галереи со ступенчатым сводом, по которой, по мысли Удена, проходил спиральный пандус, было слишком затратно. В изданной в прошлом году книге «Мир строителей пирамид. Эпоха Древнего царства» Орехов предположил, что спиральный пандус для подъема камней на верхние ярусы в пирамиде был, но не внутри специально устроенной галереи, а открытый. Блоки по самому краю ярусов располагали горизонтально, что было необходимо для устойчивости конструкции (поэтому наружная кладка, которую мы видим, выглядит параллельной основанию), а следующие несколько рядов каменной массы укладывали вдоль граней на том же уровне, но под наклоном, образуя «серпантин». Транспортировочный пандус образовывал на сторонах пирамиды уступы. Но почему тогда пирамида Хуфу не выглядит ступенчатой? Когда, дойдя до последнего яруса сооружения, строители установили верхушку-пирамидион, то, двигаясь сверху вниз, стали закладывать эти уступы каменной массой, чтобы получился пологий склон. Одновременно рабочие укладывали верхние ряды облицовки, окончательно выравнивая грани по пирамидиону. Блоки сложились в гладкие поверхности, расходившиеся под точным углом от вершины первого из семи чудес света и скрывшие на 4000 лет хитроумную идею древних строителей.
Строители
20 000 на зарплатеПо словам Геродота, на подготовку к сооружению пирамиды Хуфу потребовалось 10 лет, а на строительство — 20, и рабочие трудились в три смены по 100 000 человек. Современные исследователи, опираясь прежде всего на данные археологии, предполагают, что на стройке было занято 20 000–25 000 человек. Силы тем не менее внушительные: по масштабам Древнего мира это численность населения крупного города.Считается, что стройкой века руководил придворный зодчий — Хемиуну (по данным разных исследователей, родной или двоюродный брат Хуфу).
На ней трудились не рабы, а свободные подданные фараона, получавшие за работу плату и еду. Их поселения и могилы раскопаны археологами неподалеку от царских гробниц Гизы.
Рабочие жили с семьями в глинобитных хижинах, в их поселках были пекарни и пивоварни, лавки и склады, кузницы и административные здания.
Строителей делили на отряды численностью до 1000 человек, носившие красивые названия в честь фараона: «Хуфу пробуждает любовь», «Белая корона Хуфу могуча» и т. д.
Николай ФедоровИллюстрации: Андрей Дорохин
Понравился наш сайт? Присоединяйтесь или подпишитесь (на почту будут приходить уведомления о новых темах) на наш канал в МирТесен!
Источник: https://7lostworlds.ru/blog/43566592760/prev
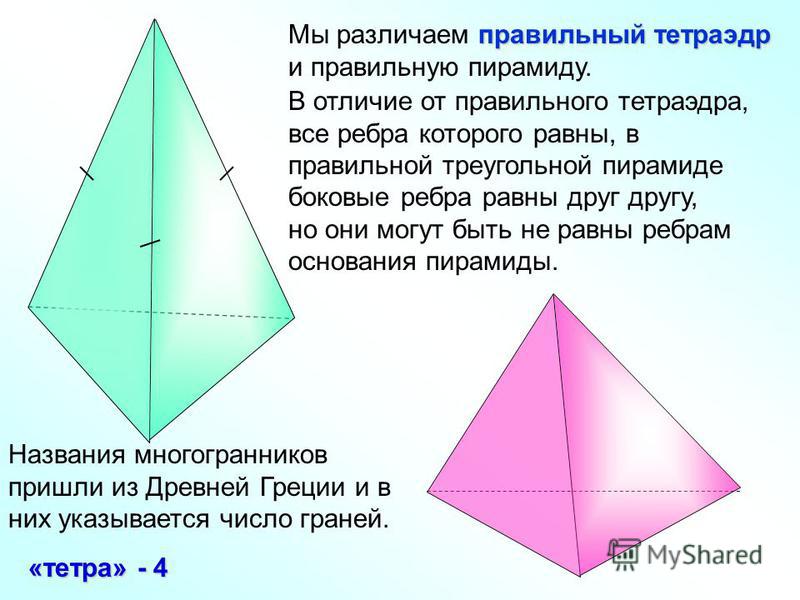
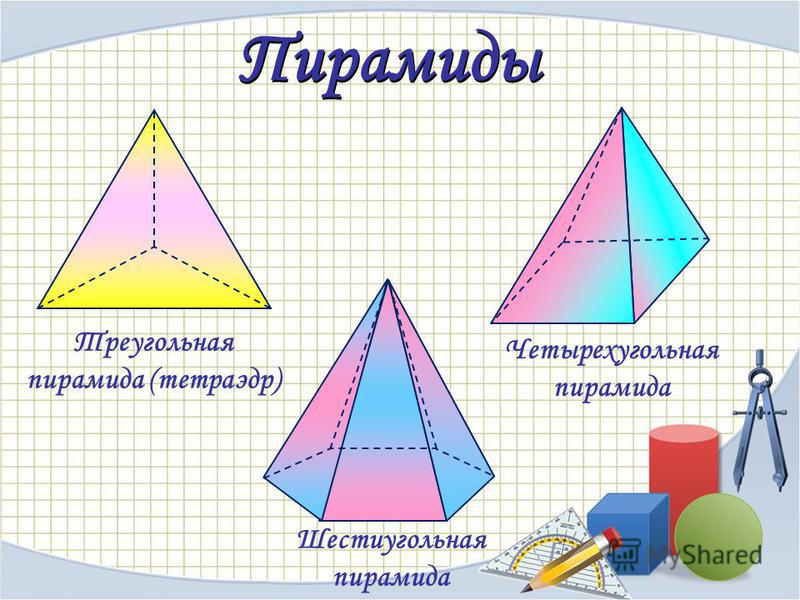
– Какие тела называются многогранниками?
1<\p>
2<\p>
3<\p>
4 — Какие тела называются многогранниками? — Какие тела относятся к телам вращения? — Чем отличается призма от пирамиды, от усечённой пирамиды? — Чем отличается цилиндр от конуса, от усечённого конуса? — Перечислите элементы следующих геометрических тел: конуса, цилиндра, призмы, пирамиды.<\p>
5 — Какие тела называются многогранниками?<\p>
6 Многогранниками, или гранными геометрическими телами называют часть пространства, ограниченную несколькими плоскостями. Призма правильная — это многогранник, у которого два основания — одинаковые взаимно параллельные грани (многоугольники), и боковые грани — прямоугольники, перпендикулярные основанию. Пирамида — это многогранник, у которого одна грань — многоугольник — принимается за основание, остальные грани (боковые) — треугольники с общей вершиной, называемой вершиной пирамиды. Усечённая пирамида — это многогранник, у которого два основания — многоугольники разного размера, и боковые грани — трапеции<\p>
7 Геометрические тела вращения.<\p>
8 M =M = L раб. поля — (297 — 25) — (l дет. + а дет.) 3<\p>
9 Выбор положения формата и масштаба изображения. 1. Если высота детали h больше длины a, положение формата выбираем вертикальным — с основной надписью по короткой стороне. 2. Если длина детали a больше высоты h, положение формата выбираем горизонтальным — с основной надписью по длинной стороне.<\p>
10 Расчёт рабочего поля чертежа по горизонтальному направлению: L — длина рабочего поля чертежа = 210 — (20 + 5) = 185 l — длина детали a — ширина детали Расчёт рабочего поля чертежа по вертикальному направлению: H — высота рабочего поля чертежа = 297 — (5 + 5) = 287 h — высота детали а — ширина детали ПОЛОЖЕНИЕ ФОРМАТА — ВЕРТИКАЛЬНОЕ M =M = L раб. поля — (210 — 25) — (l дет. + а дет.) 3 N = H раб.поля (297 — 10) — (h дет. + а дет.) 3<\p>
11 l деталиMMM N N N a детали h детали a детали Вертикальное положение формата<\p>
12 N = H раб.поля (210 — 10) — (h дет. + а дет.) 3 Расчёт рабочего поля чертежа по вертикальному направлению: H — высота рабочего поля чертежа = 210 — (5 + 5) = 200 h — высота детали а — ширина детали Расчёт рабочего поля чертежа по горизонтальному направлению: L — длина рабочего поля чертежа = 297 — (20 + 5) = 272 l — длина детали a — ширина детали M =M = L раб. поля — (297 — 25) — (l дет. + а дет.) 3<\p>
13 МММ N N N Длина детали l Ширина детали a Ширина детали a Высота детали h Горизонтальное положение формата<\p>
14<\p>
15<\p>
16<\p>
17 Тема урока׃ проекции вершин, ребер и граней предмета. Цель урока׃ нахождение на чертеже вершин, рёбер, граней, образующих и поверхностей тел, предмета. Урок 23<\p>
18 Проекции (изображения) любых, самых простых объектов окружающего нас мира состоят из простейших геометрических элементов: вершин, рёбер, кривых поверхностей, образующих, граней и т.п. Изображение любого предмета сводится к изображению вершин, рёбер, граней, кривых поверхностей. Рассмотрим процесс образования предмета как процесс изображения отдельных геометрических элементов его составляющих.<\p>
19<\p>
20 V H W Вид сверху Вид спереди Вид слева<\p>
21 V H W Z X Y<\p>
22 V H W Z X Y<\p>
23<\p>
24 V H W Z X Y<\p>
25 V H W Z X Y Сторона а = Высота h = Фамилия, имя: Класс: Задание: 1.Построить прямоугольное основание. 2. Построить параллелепипед<\p>
26 V H W Z X Y Фамилия, имя: Класс: a h Сторона а = Сторона b = Высота h = b Задание: 1.Построить трапецеидальное основание. 2. Построить призму<\p>
27 V H W Z X Y Сторона а = Высота h = Фамилия, имя: Класс: Задание: 1.Построить треугольное основание. 2. Построить призму а<\p>
28 V H W Z X Y Сторона а = Сторона b = Высота h = Фамилия, имя: Класс: Задание: 1.Построить прямоугольное основание. 2. Построить параллелепипед<\p>
29 V H W Z X Y Сторона а = Диагональ с = Апофема s = Высота h = с s Фамилия, имя: Класс: Задание: 1.Построить шестиугольное основание. 2. Построить призму<\p>
30 V H W Z X Y<\p>
31 V H W Z X Y<\p>
32<\p>
33 Построение осей в изометрической проекции XY Z YX<\p>
34<\p>
35<\p>
36 30º<\p>
37 Грань параллельная плоскости проекции, проецируется на эту плоскость в натуральную величину. На две другие плоскости проекций эта грань проецируется в линию. Рассмотрим три случая расположения граней относительно плоскостей проекций: 1. Проецирующая грань параллельна (II) фронтальной плоскости проекций V (ABCD II V) 2. Проецирующая грань параллельна (II) горизонтальной плоскости проекций H (АВСD II H). 3. Проецирующая грань параллельна (II) профильной плоскости проекций W (ABCD II W)<\p>
38 V H W Z X Y A B C D a b d c a,d b,c d,c a,b 1.Проецирующая грань параллельна (II) фронтальной плоскости проекций V (ABCD II V)<\p>
39 V H W Z X Y A B b d a,d b,c a,b d,c C D c a b 2. Проецирующая грань параллельна (II) горизонтальной плоскости проекций H (АВСD II H).<\p>
40 V H W Z X Y A B C D A a,d b,c a b a,b c,d c d 3. Проецирующая грань параллельна (II) профильной плоскости проекций W (ABCD II W)<\p>
41 Алгоритм построения наклонной плоскости, то есть плоскости, которая не параллельна ни одной плоскости проекций.<\p>
42 V H W Z X Y A B C D a,d b,c b c a d c a b d Алгоритм построения наклонной плоскости, то есть плоскости, которая не параллельна ни одной плоскости проекций.<\p>
43<\p>
44 n n n m mm l h b b<\p>
45<\p>
46<\p>
47<\p>
48<\p>
49 V H W Z X Y<\p>
50<\p>
51<\p>
52 V H W Z X Y<\p>
53<\p>
54<\p>
55<\p>
56<\p>
57 ГРАНИ ПАРАЛЛЕЛЕПИПЕДА<\p>
58 Рассмотрим составляющие элементы геометрической формы — прямоугольной призмы или параллелепипеда<\p>
59<\p>
60 ГРАНЬ –<\p>
61 a B D V V А b C c d H H a,b c,d E F e,k W Wb a G e g (K),gf,e,g,f,d,k,c,k,f<\p>
62 РАЗВЁРТКА ШЕСТИГРАННОЙ ПРИЗМЫ<\p>
63<\p>
64<\p>
65<\p>
66<\p>
67 Развертка трёхгранной призмы<\p>
68<\p>
69 Развёртка шестигранной пирамиды<\p>
70<\p>
71 РАЗВЁРТКА ШЕСТИГРАННОЙ ПИРАМИДЫ ГРАНИ ПИРАМИДЫ ОСНОВАНИЕ<\p>
72 РАЗВЁРТКА ЦИЛИНДРА<\p>
73 ЦИЛИНДР. РАЗВЕРТКА ЦИЛИНДРА ОСНОВАНИЯ ЦИЛИНДРА ОБРАЗУЮЩАЯ ЦИЛИНДРА<\p>
74 РАЗВЁРТКА КОНУСА<\p>
75 РАЗВЁРТКА ПРЯМОУГОЛЬНОЙ ПРИЗМЫ<\p>
76 ПИРАМИДА — ГЕОМЕТРИЧЕСКОЕ ТЕЛО, У КОТОРОГО ОСНОВАНИЕ МНОГОУГОЛЬНИК, А БОКОВЫЕ ГРАНИ — ТРЕУГОЛЬНИКИ, ИМЕЮЩИЕ ОБЩУЮ ВЕРШИНУ Вершина Ребро Грань<\p>
77 Высота пирамиды Основание<\p>
78<\p>
79<\p>
80<\p>
81<\p>
82<\p>
83<\p>
84<\p>
85<\p>
86 ГЕОМЕТРИЧЕСКИЕ ТЕЛА И ИХ ЭЛЕМЕНТЫ ПРИЗМА КОНУС УСЕЧЁННЫЙ КОНУС ЦИЛИНДР ПИРАМИДА<\p>
87 ОСНОВАНИЯ ГРАНИ<\p>
88 РЁБРА ВЕРШИНА<\p>
89 Ребро — это линия пересечения двух плоскостей (граней) РЁБРА<\p>
90 А B C D E F G N K ВЕРШИНА — точка пересечения рёбер или граней, или точка схода образующей конуса ВЕРШИНА<\p>
91 Грани пирамиды Рёбра пирамиды Вершина пирамиды Вершина, рёбра и грани пирамиды<\p>
92 Проекции точки, лежащей на поверхности (грани) пирамиды<\p>
93 Кривая поверхность — ОСНОВАНИЕ КОНУСА Очерковая образующая конуса Вершина конуса Вершина, кривая поверхность и образующая конуса<\p>
94 R Построение проекции точки на поверхности конуса (усечённого ) А а a a R<\p>
95 R Алгоритм построения проекции точки на поверхности конуса А а a a R B b b b<\p>
96 Цилиндр и его составляющие элементы Очерковая образующая бразующая цилиндра Кривая поверхность — основания цилиндра<\p>
97 Алгоритм построения проекции точки на поверхности цилиндра А aa a<\p>
98<\p>
99 АГОРИТМ ПОСТРОЕНИЯ ПРОЕКЦИЙ ТОЧЕК НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ ДЕТАЛИ 1. Анализ геометрической формы детали и её симметричности. 2. Установление геометрической формы детали, на поверхности которой задана точка. 3. Определение видимости каждой геометрической формы на заданных видах детали. 4. Построение проекций точки на каждой геометрической форме по рассмотренному выше алгоритму и их обозначение с учётом видимости.<\p>
100 1. Анализ геометрической формы детали и её симметричности. Предметы окружающие нас имеют форму геометрических тел или представляют их сочетания<\p>
101 В основе формы деталей машин и механизмов находятся геометрические тела, т.е. они представляют собой совокупность геометрических тел. Мысленное расчленение предмета на составляющие его геометрические тела называют анализом геометрической формы<\p>
102<\p>
103 Получение детали методом удаления простейших геометрических форм<\p>
104 Наглядное изображение получения детали<\p>
105<\p>
106 (a) a a Проекции точки на поверхности предмета А<\p>
107 Аксонометрическая проекция предмета<\p>
108 Алгоритм построения точки на комплексном чертеже предмета<\p>
109 Алгоритм построения чертежа детали, представленного тремя видами. V W H<\p>
110<\p>
111 1. Анализ геометрической формы детали и её симметричности. 2. Выбор главного вида (вида спереди), вида сверху и вида слева. 3. Выбор положения формата и масштаба изображения. 4. Установление рабочего поля чертежа: расчет и построение габаритных прямоугольников, проведение осей симметрии. 5. Построение очертания главного вида. 6. Построение очертания вида сверху. 7. Построение очертания вида слева. 8. Нанесение размеров. 9. Обводка контура изображения детали сплошной толстой линией. 10.Заполнение основной надписи. 11.Проверка чертежа.<\p>
112 Построение проекционных прямоугольников по габаритным размерам детали.<\p>
113<\p>
114<\p>
115<\p>
116<\p>
117<\p>
118<\p>
119<\p>
120<\p>
121 А Алгоритм построения точки на поверхности предмета a (a) a V W W V H H b b b B<\p>
122<\p>
123 А B C D E<\p>
124 d b А B C D E V V Z X<\p>
125 a c А B C D E H H X Y<\p>
126 e<\p>
127 А B C D E e Z Y W W<\p>
128 А B C D E<\p>
129 А B C D E<\p>
130 ee e a aa b b b d d d c c c x z y y H W V<\p>
131<\p>
132<\p>
133<\p>
134<\p>
135<\p>
136<\p>
137<\p>
138<\p>
139<\p>
140<\p>
141<\p>
142<\p>
143<\p>
144<\p>
145<\p>
146<\p>
147<\p>
148<\p>
149<\p>
Источник: http://www.myshared.ru/slide/200251
ПОИСК
 Внутренняя структура молекул воды. Молекулы воды состоят из водорода и кислорода. С современных позиций строения атома электронные облака молекул воды расположены в форме неправильного тетраэдра.
Внутренняя структура молекул воды. Молекулы воды состоят из водорода и кислорода. С современных позиций строения атома электронные облака молекул воды расположены в форме неправильного тетраэдра.
Атом кислорода оказывается при этом в центре, а два атома водорода — в противоположных углах одной из граней куба. Угол между ними составляет 104°ЗГ. Два из восьми электронов атома кислорода расположены около ядра, два других связаны с атомами водорода, а две неподеленные пары [c.
8]
Тетрагональное плоское Неправильный тетраэдр Тригональная би-пирамида [c.250]
Тетраэдрическая модель, выдвинутая в 1874 г. Вант-Гоф-фом в виде гипотезы в настоящее время вытекает из данных эксперимента. Методами рентгенографии, электронографии и др.
определяют валентные углы и междуатомные расстояния (длины связей). Если все четыре заместителя одинаковы (СН4, ССи), то модель представляет собой правильный тетраэдр с валентными углами 109° 28.
Если с центральным углеродным атомом связаны неодинаковые заместители, то валентные углы могут на несколько градусов отклоняться от тетраэдрических разными оказываются и длины связей — тетраэдр становится неправильным. Примером такого дефор- [c.14]
Тригональная бипирамида 5 4 0 1 Тригональная бипирамида Неправильный тетраэдр Примеры неизвестны [c.213]
Авторы подчеркивали, что гипотеза, выдвинутая ими для объяснения геометрической изомерии азотсодержащих соединений, основывается на следующем предположении Три валентности атома азота в некоторых соединениях направлены к углам (в общем случае неправильного) тетраэдра, четвертый угол которого занимает сам атом азота [c.235]
Прецизионные исследования при различных температурах показали, что тетраэдр, хотя и близок к идеальному, но все же несколько отличается от такового.
Две связи 51—О, обращенные к более круто наклоненному (в проекции на плоскость (0001) более короткому) ребру О—О, оказались несколько короче ( 0,1597 нм), чем связи, обращенные к противоположному более пологому ребр (0,1617 нм).
Указанная неправильность тетраэдра весьма интересна с точки зрения возможного объяснения некоторых особенностей роста кристаллов кварца, распределения зарядов при пьезоэффекте и также при изучении парамагнитных характеристик кварца, о чем более подробно сказано ниже.
Углы О—51—О также близки к идеальному тетраэдрическому и составляют 0)51102— 110,39°. Угол 51—О—51 при комнатной температуре равен 143,9°. [c.81]
Ле Бель и в особенности Вант-Гофф поэтому сочли возможным предположить, что четыре группы, связанные с одним углеродным атомом, должны быть расположены не в одной плоскости.
Если это расположение симметрично, то оно является правильно тетраэдрическим, т. е, четыре заместителя занимают углы правильного тетраэдра, в центре которого находится атом углерода.
Если расположение -несимметрично, то заместители занимают углы неправильного тетраэдра. [c.131]
В стекле правильная взаимная ориентация тетраэдров отсутствует и углы 81—О—81 не постоянны. Отклонения в значениях углов между тетраэдрами невелики, и некоторая правильность в расположении соседних тетраэдров сохраняется.
Но даже при незначительной неправильности во взаимной ориентации тетраэдров по мере удаления пх друг от друга нарушения накапливаются и тетраэдры оказываются ориентированными произвольным образом (рис. 121). [c.
192]
Менее упорядоченное расположение тетраэдров приводит к нарушениям симметрии и периодичности, сетка становится искаженной, неправильной. Такая сетка обладает энергией, мало отличающейся от энергии кристалла. [c.192]
Пользуясь принципом построения изотермической диаграммы растворимости тройной системы в плоском прямоугольном треугольнике (см. рис. 5.
32), можно изотерму простой четверной системы из воды А и трех солей В, С и О изобразить в лежащей на одной из боковых граней пирамиде, боковые грани которой имеют прямой угол у ее вершины (неправильный тетраэдр, см. поз. 5 на рис. 5.4). На рнс. 5.
57 изображена такая пространственная изотерма для случая, когда в системе отсутствуют кристаллогидраты, двойные и тройные соли. Вдоль трех координатных осей, пересекающихся под прямыми углами, отлажены концентрации солей в системе (в процентах). Масштабы этих осей могут быть неодинаковыми.
Вершина пирамиды А является ее водным углом. Отдельные элементы пространственной фигуры тождественны рассмотренным выше элементам аналогичной фигуры в правильном тетраэдре (ср. рис. 5.49). [c.178]
Плоский треугольник Плоский треугольник Плоский треугольник Плоский треугольник Несимметрично на плоскост Треугольная пирамида. Треугольная пирамида. Тетраэдрическое. … Тетраэдрическое. … Плоский четырехугольник Плоский четырехугольник Неправильный тетраэдр. Неправильный тетраэдр Неправильный тетраэдр. Тетра ональная пирамида [c.306]
Рентгенографическим летодом установлено, что молекула реактива Гриньяра, выделенная в твердом состоянии из эфирного раствора, представляет собой диэфират (3), имеющий структуру неправильного тетраэдра, в центре которого находится атом магния (изображен диэфират этилмагнийбромида, [c.259]
Моноалюминат кальция СаО-АЬОз является основным минералом глиноземистого клинкера. Его структура соответствует структуре -тридимита, в которой все атомы кремния замещены атомами алюминия. Это обусловливает необычное трехмерное размещение тетраэдров. Структура сильно искажена большими ионами кальция.
Два из трех ионов кальция координированы шестью ионами кислорода, а третий окружен девятью ионами кислорода. Соответственно расстояние Са—О для Са и Саг изменяется от 0,231 до 0,272 нм, а для Саз — от 0,236 до 0,317 нм. Этим объясняется высокая гидратационная активность СА.
Этот минерал кристаллизуется в виде зерен призматической и неправильной формы с отрицательным погасанием, характеризующихся двуосностью, 2V=36°. Показатели их преломления следующие 1,643 [c.243]
Хорошим катализатором при синтезе хлористого. сульфурила (т. пл. —54, т. кип. 69 °С) является камфора. Молекула O2S I2 полярна (р.
= 1,80), а ее пространственное строение отвечает неправильному тетраэдру с параметрами (80) = = 1,41 А, Z080 = 123°, d(8 l) = 2,01 А, Z 18 1 = 100°. При нагревании выше 300 °С хлористый сульфурил распадается на 802,и СЬ.
Он является хорошим растворителем для 80з и большинства хлоридов многовалентных металлов. Взаимодействие [c.334]
Все атомы углерода в алканах имеют кр -гибридиза-цию, т. е. одна s- и три р-орбитали внешнего электронного уровня смешиваются и образуют четыре зр -габридные орбитали одинаковой формы (неправильные объемные восьмерки), направленные в раз 1ые стороны пространства под углом 109.5 .
Эти гибридные орбитали образуют четыре а-связи с другими атомами углерода или водорода, sp -гибридизованный углерод называют также тетраэдрическим, так как если его поместить в центр чстырсхграниоУ пирамиды (тетраэдра), то его связи будут направлены к вершинам этого тетраэдра. [c.
126]
На рис. 5.17 изображена структура молекул 8р4, С1Рз и 1С1 а, которые принадлежат к типу АХ Е, АХ Е2 и АХ Ез соответственно.
Ясно видно, что наличие у центрального атома неподеленной пары придает молекуле 8р4 форму неправильного тетраэдра две пары неподеленных электронов молекулы С1Рз приводят к Т-образной форме этой молекулы.
Ион 1С1 2, центральный атом которого (атом иода) имеет три неподеленные пары, обладает линейной формой. [c.144]
Еще в 1932 г. В. Г. Захариассен предположил, что структуру аморфного SIO2 можно имитировать моделью беспорядочной сетки, в которой каждый атом кремния находится в центре тетраэдра, а атомы кислорода — в его вершинах. Параметры этой сетки были уточнены Б. Уорреном на основании анализа кривой распределения функции пар атомов.
Он констатировал, что рентгеновские результаты полностью объясняются, если представить структуру аморфного кремнезема в виде неправильной сетки, где каждый атом кремния находится в тетраэдрическом окружении четырех атомов кислорода, а каждый атом кислорода связан с двумя атомами кремния. Вокруг направления связи Si-7-0 ориентация тетраэдров беспорядочная.
[c.315]
Модель неправильного тетраэдра у Пастера относилась к молекуле виппой кислоты, а не к атому углерода. [c.214]
С пространственными (стерггаескимн) факторами мы постоянно будем сталкиваться в следуюшцх главах этой книги. Они искажают симметрию молекулы (например, превращают тетраэдр в неправильную фигуру), препятствуют свободному вращению вокруг ст-связей, сильно влияют на [c.84]
Классифицируют П с по строению остова Остов м б в виде правипьного потиэдра, напр тетраэдр, куб, октаэдр и т д, и неправильного полиэдра, напр призма, тригональная бипирач
Источник: http://chem21.info/info/761622/
Объем данного правильного тетраэдра 2. Правильные ответы. KakPravilno-Sdelat.ru

Рассмотрим произвольный треугольник ABC и точку D. не лежащую в плоскости этого треугольника. Соединим отрезками эту точку с вершинами треугольника ABC. В результате получим треугольники ADC. CDB. ABD.
Поверхность ограниченная четырьмя треугольниками ABC. ADC. CDB и ABD называется тетраэдром и обозначается DABC.
Треугольники, из которых состоит тетраэдр, называются его гранями.
Стороны данных треугольников называют ребрами тетраэдра.
А их вершины — вершинами тетраэдра
Тетраэдр имеет 4 грани. 6 ребер и 4 вершины . Два ребра, которые не имеют общей вершины, называются противоположными.
Зачастую для удобства, одну из граней тетраэдра называют основанием. а оставшиеся три грани боковыми гранями.
Таким образом, тетраэдр — это простейший многогранник, гранями которого являются четыре треугольника.
Но также верно и утверждение, что любая произвольная треугольная пирамида является тетраэдром. Тогда также верно, что тетраэдром называют пирамиду, в основании которой лежит треугольник.
Высотой тетраэдра называется отрезок, который соединяет вершину с точкой, расположенной на противоположной грани и перпендикулярный к ней.
Медианой тетраэдра называется отрезок, который соединяет вершину с точкой пересечения медиан противоположной грани.
Бимедианой тетраэдра называется отрезок, который соединяет середины скрещивающихся ребер тетраэдра.
Так как тетраэдр — это пирамида с треугольным основанием, то объем любого тетраэдра можно рассчитать по формуле
,
- S — площадь любой грани,
- H — высота, опущенная на эту грань
Правильный тетраэдр #8212; частный вид тетраэдра
Тетраэдр, у которого все грани равносторонние треугольник называется правильным.
Свойства правильного тетраэдра:
- Все грани равны.
- Все плоские углы правильного тетраэдра равны 60
- Так как каждая его вершина является вершиной трех правильных треугольников, то сумма плоских углов при каждой вершине равна 180
- Любая вершина правильного тетраэдра проектируется в ортоцентр противоположной грани (в точку пересечения высот треугольника).
Пусть нам дан правильный тетраэдр ABCD с ребрами равными a. DH — его высота. Произведем дополнительные построения BM — высоту треугольника ABC и DM — высоту треугольника ACD . Высота BM равна BM и равна Рассмотрим треугольник BDM. где DH. являющаяся высотой тетраэдра также и высота данного треугольника.
Высоту треугольника, опущенную на сторону MB можно найти, воспользовавшись формулой
Таким образом формула объема для правильного тетраэдра
где a –ребро тетраэдра
Вычисление объема тетраэдра, если известны координаты его вершин
Геометрических смысл смешенного произведения трех векторов заключается в следующем — смешенное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах.
Так как тетраэдр есть пирамида с треугольным основанием, а объем пирамиды в шесть раз меньше объема параллелепипеда, то тогда имеет смысл следующая формула
Примечание. Это часть урока с задачами по геометрии (раздел стереометрия, задачи о пирамиде). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме.
В задачах вместо символа квадратный корень применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение.
Для простых подкоренных выражений может использоваться знак .
Теория
(теоретические сведения см. также в уроке Правильный тетраэдр )
Правильный тетраэдр — это правильная треугольная пирамида у которой все грани являются равносторонними треугольниками.
У правильного тетраэдра все двугранные углы при рёбрах и все трёхгранные углы при вершинах равны
У тетраэдра 4 грани, 4 вершины и 6 ребер.
Основные формулы для правильного тетраэдра приведены в таблице. Где: S — Площадь поверхности правильного тетраэдра V — объем h — высота, опущенная на основание r — радиус вписанной в тетраэдр окружности R — радиус описанной окружности a — длина ребра
Практические примеры
Задача.
Найдите площадь поверхности треугольной пирамиды, у которой каждое ребро равно √3
Решение. Поскольку все ребра треугольной пирамиды равны — она является правильной. Площадь поверхности правильной треугольной пирамиды равна S = a 2 √3. Тогда
S = 3√3
Задача. Все ребра правильной треугольной пирамиды равны 4 см. Найдите объем пирамиды
Решение.
Поскольку в правильной треугольной пирамиде высота пирамиды проецируется в центр основания, который одновременно является центром описанной окружности, то
AO = R = √3 / 3 a
AO = 4√3 / 3
Таким образом, высота пирамиды OM может быть найдена из прямоугольного треугольника AOM
AO 2 + OM 2 = AM 2 OM 2 = AM 2 — AO 2 OM 2 = 4 2 — ( 4√3 / 3 ) 2 OM 2 = 16 — 16/3 OM = √(32/3)
OM = 4√2 / √3
Объем пирамиды найдем по формуле V = 1/3 Sh
При этом площадь основания найдем по формуле S = √3/4 a 2
V = 1/3 (√3 / 4 * 16 ) ( 4√2 / √3 )
V = 16√2 / 3
Ответ. 16√2 / 3 см
Решение задач с пирамидами (разные задачи)!
Здравствуйте, Дорогие друзья! В данной статье продолжим рассматривать задачи с пирамидами. Их нельзя отнести к какому-то классу или типу заданий, и дать общие рекомендации для решения. Я просто собрал оставшиеся задачи, не рассматриваемые ранее, и решил изложить их в одной статье.
Перечислю теорию, которую необходимо освежить в памяти перед решением: формула объёма пирамиды, свойства подобия фигур и тел, свойства правильных пирамид, теорема Пифагора, формула площади треугольника (в этой статье она вторая). Рассмотрим задачи:
От треугольной пирамиды, объем которой равен 80, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
Объём пирамиды равен одной трети произведения площади её основания и высоты:
Данные пирамиды (исходная и отсечённая) имеют общую высоту, поэтому их объемы соотносятся как площади их оснований. Средняя линия от исходного треугольника отсекает треугольник площадь которого в четыре раза меньше, то есть:
Подробнее об этом можно посмотреть здесь.
Это означает, что объём отсечённой пирамиды будет в четыре раза меньше.
Таким образом, он будет равен 20.
* Посмотрите решение аналогичной задачи, использована формула площади треугольника.
Объем треугольной пирамиды равен 15. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1. 2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду.
Постоим пирамиду, обозначим вершины. Отметим на ребре AS точку Е, так чтобы AE была в два раза больше ES (в условии сказано, что ES относится к AE как 1 к 2), и построим указанную плоскость проходящую, через ребро АС и точку Е:
Проанализируем объём какой пирамиды будет больше: EABC или SEBC?
*Объём пирамиды равен одной трети произведения площади её основания и высоты:
Если рассмотреть две полученные пирамиды и в обеих принять за основание грань ЕВС, то становится очевидно, то объём пирамиды АЕВС будет больше объёма пирамиды SEBC. Почему?
Расстояние от точки А до плоскости ЕВС больше чем расстояние от точки S. А это расстояние играет у нас роль высоты.
Итак, найдём объём пирамиды ЕАВС.
Объём исходной пирамиды нам дан, основание у пирамид SАВС и ЕАВС общее. Если мы установим соотношение высот, то без труда сможем определить объём.
Из отношения отрезков ES и AE следует, что АЕ равно две третьих ES. Высоты пирамид SАВС и ЕАВС находятся в такой же зависимости — высота пирамиды ЕАВС будет равна 2/3 высоты пирамиды SАВС.
Таким образом, если
Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.
В правильной пирамиде вершина проецируется в центр основания. Выполним дополнительные построения:
Найти боковое ребро мы можем из прямоугольного треугольника SOC. Для этого нужно знать SO и ОС.
SO это высота пирамиды, её мы можем вычислить используя формулу объёма:
Вычислим площадь основания. это правильный шестиугольник со стороной равной 1. Площадь правильного шестиугольника равна площади шести равносторонних треугольников с такой же стороной, подробнее об этом изложено здесь (п.6), итак:
ОС = ВС = 1, так как в правильном шестиугольнике отрезок соединяющий его центр с вершиной равен стороне этого шестиугольника.
Таким образом, по теореме Пифагора:
Объ ем тетраэдра равен 200. Найдите объем многогранника, вершинами которого являются середины ребер данного тетраэдра.
Объем указанного многогранника равен разности объемов исходного тетраэдра V0 и четырех равных тетраэдров, каждый из которых получается отсечением плоскостью, проходящей через середины рёбер, имеющих общую вершину:
Определим, чему равен объём отсеченного тетраэдра.
Отметим, что исходный тетраэдр и «отсечённый» тетраэдр являются подобными телами. Известно, что отношение объёмов подобных тел равно k 3. где k — коэффициент подобия. В данном случае он равен 2 (так как все линейные размеры исходного тетраэдра в два раза больше соответствующих размеров отсечённого):
Вычислим объём отсечённого тетраэдра:
Таким образом, искомый объём будет равен:
Площадь поверхности тетраэдра равна 120. Найдите площадь поверхности многогранника, вершинами которого являются середины ребер данного тетраэдра.
Искомая поверхность состоит из 8 равносторонних треугольников со стороной, вдвое меньшей ребра исходного тетраэдра. Поверхность исходного тетраэдра состоит из 16-ти таких треугольников (на каждой из 4 граней тетраэдра по 4 треугольника), поэтому искомая площадь равна половине площади поверхности данного тетраэдра и равна 60.
Так как известна площадь поверхности тетраэдра, то мы можем найти его ребро, затем определить длину ребра многогранника и далее вычислить площадь его поверхности.
Площадь поверхности тетраэдра состоит из четырёх равных по площади правильных треугольников. Пусть сторона такого треугольника (ребро тетраэдра) равна а, тогда можем записать:
Ребра многогранника равны его половине ребра тетраэдра, то есть:
*Они проходят через середины рёбер тетраэдра.
Многогранник имеет восемь равных граней являющихся правильными треугольниками, значит его площадь поверхности будет равна:
*Данное решение алгебраическое и рациональным его назвать никак нельзя, представлено как альтернативный вариант.
27115. От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
27175. Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер.
27214. Объем тетраэдра равен 1,9. Найдите объем многогранника, вершинами которого являются середины ребер данного тетраэдра.
А теперь для поднятия настроения ролик. Оказывается, что песня не только людей объединяет, но и животных
Источник: http://www.kak-sdelatpravilno.ru/pravilnye-otvety/obem-dannogo-pravilnogo-tetrajedra-2.html
Пирамида. Виды пирамид

Определение 1
Геометрическая фигура, образованная многоугольником и точкой, не лежащей в плоскости, содержащей этот многоугольник, соединенной со всеми вершинами многоугольника называется пирамидой (рис. 1).
Пирамида”>
Рисунок 1. Пирамида
Многоугольник, из которого составлена пирамида, называется основанием пирамиды, получаемые при соединение с точкой треугольники — боковыми гранями пирамиды, стороны треугольников — сторонами пирамиды, а общая для всех треугольников точка– вершиной пирамиды.
В зависимости от количества углов в основании пирамиды ее можно назвать треугольной, четырехугольной и так далее (рис. 2).
Рисунок 2.
Еще один вид пирамид — правильная пирамида.
Определение 2
Пирамида, в основании которой лежит правильный многоугольник и высота пирамиды падает в его центр называется правильной пирамидой (рис. 3).
Рисунок 3. Правильная пирамида
Введем и докажем свойство правильной пирамиды.
Теорема 1
Все боковые грани правильной пирамиды являются равнобедренными треугольниками, которые равны между собой.
Доказательство.
Рассмотрим правильную $n-$угольную пирамиду с вершиной $S$ высотой $h=SO$. Опишем вокруг основания окружность (рис. 4).
Рисунок 4.
Рассмотрим треугольник $SOA$. По теореме Пифагора, получим
[AS=sqrt{{AO}^2+{SO}^2}=sqrt{R^2+h^2}]
Очевидно, что так будет определяться любое боковое ребро. Следовательно, все боковые ребра равны между собой, то есть все боковые грани — равнобедренные треугольники. Докажем, что они равны между собой. Так как основание — правильный многоугольник, то основания всех боковых граней равны между собой. Следовательно, все боковые грани равны по III признаку равенства треугольников.
Теорема доказана.
Ничего непонятно?
Попробуй обратиться за помощью к преподавателям
Введем теперь следующее определение, связанное с понятием правильной пирамиды.
Определение 3
Апофемой правильной пирамиды называется высота её боковой грани.
Очевидно, что по теореме один все апофемы равны между собой.
Теорема 2
Площадь боковой поверхности правильной пирамиды определяется как произведение полупериметра основания на апофему.
Доказательство.
Обозначим сторону основания $n-$угольной пирамиды через $a$, а апофему через $d$. Следовательно, площадь боковой грани равна
[s=frac{1}{2}ad]
Так как, по теореме 1, все боковые стороны равны, то
[S_{бок}=frac{1}{2}and=frac{P_{осн}}{2}d]
Теорема доказана.
Еще один вид пирамиды — усеченная пирамида.
Определение 4
Если через обычную пирамиду провести плоскость, параллельную её основанию, то фигура, образованная между этой плоскостью и плоскостью основания называется усеченной пирамидой (рис. 5).
Рисунок 5. Усеченная пирамида
Боковыми гранями усеченной пирамиды являются трапеции.
Теорема 3
Площадь боковой поверхности правильной усеченной пирамиды определяется как произведение суммы полупериметров оснований на апофему.
Доказательство.
Обозначим стороны оснований $n-$угольной пирамиды через $a и b$ соответственно, а апофему через $d$. Следовательно, площадь боковой грани равна
[s=frac{1}{2}(a+b)d]
Так как все боковые стороны равны, то
[S_{бок}=frac{1}{2}(a+b)nd=frac{sum{P_{осн}}}{2}d]
Теорема доказана.
Пример задачи
Пример 1
Найти площадь боковой поверхности усеченной треугольной пирамиды, если она получена из правильной пирамиды со стороной основания 4 и апофемой 5 путем отсечения плоскостью, проходящей через среднюю линию боковых граней.
Решение.
По теореме о средней линии получим, что верхнее основание усеченной пирамиды равно $4cdot frac{1}{2}=2$, а апофема равна $5cdot frac{1}{2}=2,5$.
Тогда, по теореме 3, получим
[S_{бок}=frac{1}{2}left(12+6
ight)cdot frac{5}{2}=frac{90}{4}=22,5]
Ответ: $22,5$.
Источник: https://spravochnick.ru/matematika/piramida_vidy_piramid/
14- Пирамида и Платоновы тела. ТЕТРАЭДР

Магия сакральной геометрии.
Практическое значение фигур сакральной геометрии в жизни людей.
Пирамида и Платоновы тела.ТЕТРАЭДР
статьи из книги “Что говорят Махатмы”
Светлова, Жарликов. 2016 год
http://www.soznanie.com/docs/ar64_magiya_sakralnoy_geomentii.htm
Тетраэдр.
Эта фигура так же имеет право заявить о своей индивидуальности. Она самодостаточна хоть и не имеет, как Пирамида, своего зеркального отражения. Она по своему гармонична, требует к себе уважения и получает его с Нашей стороны.
Это идеальная, прагматичная фигура, которая не знает себе равных в своей среде.
Равносторонние треугольники, соединённые в одну фигуру — Тетраэдр, не имеют ни верха, ни низа, ни боковых сторон. Это очень демократичное Платоново тело. Все его грани — полноценны. Ни одна не является главенствующей.
Это очень важный момент в рассмотрении той темы, что мы взяли сегодня.
Я рад вам доложить, что все наши геометрические изыски, которые мы обсуждали в последнее время, не остаются незамеченными вашими телами, так как они напичканы большим количеством Платоновых тел, которые могли бы вписаться в любую клеточку или атом вашего тела. Я не говорю уже о больших составляющих его.
Я говорю, могли бы, потому что на самом деле ни одно тело, кроме Икосаэдра, не входит сейчас из вне, не находится в структуре Астрального тела и физического.
Но тем не менее я говорю об этом, как бы поднимаю тему, говорю о присутствии того, чего нет в реальности.
Зачем Я это делаю?
Парадокс заключается в том, что для Астрального тела и для физического не имеет значение — можно ли вписать геометрическую фигуру временно мыслеформой, умозаключительно или она постоянно присутствует в ней всей своей ипостасью.
Вся Личность от атома до целостного тела на информационном уровне состоит из геометрических фигур изначально.
Все Платоновы тела и сфера присутствуют во всех телах человека. Они являются изначальной информационной решёткой, на которой затем нарастает энергия Пространства. Притянутая ими сфера заключает все эти виды энергий в единое целое.
Вообще все округлые формы — производные сферы, окружают все многоугольники, отделяют их от Пространства, в котором они находятся. Заключают их в свои объятия, создавая определённую форму бытия.
Все геометрические фигуры в сфере разной конфигурации входят друг в друга, составляют определённый объект по программе, заложенной свыше. В этом объекте присутствуют фигуры, каждая из которых принимает энергию из Пространства в своих вибрациях. Как вы уже знаете, делает она это с помощью углов, которые в ней заложены.
– Учитель, я не могу это представить?!
Ведь формы, которые мы видим в окружающем мире и внутри себя, на уровне рассматриваемых под микроскопом клеток, очень редко соответствуют тем геометрическим фигурам, что мы рассматривает в этой статье.
Чаще всего они вообще не имеют какой-то чётко выраженной формы. Имеются ввиду естественные, а не искусственно созданные человеком формы.
Только в кристаллической среде можно увидеть их достаточно близко к идеальным.
– Да. Верно. Природа не любит сухой лаконичности и геометрической правильности. И в этом она права!
Люди не смогли бы жить, окружённые безукоризненными формами Платоновых тел. Они подавляют человека, если постоянно присутствуют в видимом мире, окружающем его. Как бы «высушивают» его мозг. Не дают размаха фантазии и творчеству, без которого он не может жить. Постоянное видение и нахождение в угловых формах, окружающих человека, очень быстро прекратит его жизнь!
Иногда делают дома с пирамидальной крышей. Помощью пирамиды следует пользоваться в ограниченном порядке. Людям в Пирамиде не стоит находиться постоянно по той причине, что выйдя из неё человек будет чувствовать себя беззащитным.
Безусловно, Пирамида вносит гармонию в само здание и в жизни людей, которые в нем живут, делает их более здоровыми и оптимистичными, но тем не менее, постоянное безвыходное, хотя бы на несколько часов, нахождение в таком доме выдёргивает человека из реалий жизни, далеко не идеальной в ваше время, и мешает адаптации к существующим в обществе условиям. Человек выглядит как бы не от мира сего. Не умеет отстаивать свои права. И общество отодвигает его в сторону.
Любая излишняя опека не даёт возможности развития внутренней силе человека. В то время, как неприятные препятствия развивают и укрепляют его стойкость!
И в то же время, если крыша пирамидальной формы находится над административным зданием, где решаются важные для жизни общества вопросы, то результат работы будет наиболее приближен к идеалу и деятельность в таком здании будет двигать жизнь в более гармоничном и справедливом направлении.
Когда вы будет работать над собой, над улучшением своего физического состояния с помощью Пирамиды, то при определённой просьбе Пирамида, как самая мощная и гармоничная фигура, будет влиять на ту решётку геометрическую, из которой состоят ваши атомы, клетки, органы, части тела и жидкость, что находится в вашем теле.
Орган не может восстановить свою нормальную форму, деятельность и здоровье ещё и по той причине, что под воздействием различных отрицательных для него факторов решётка адаптировалась, подчинилась тем условиям, в которые попал орган и перестала соответствовать изначальному стандарту !
При этом состояние органа (части тела, жидкости) не является нормальным, здоровым и гармоничным. Зная об этом или предполагая подобную ситуацию, можно поставить на Пирамиду соответствующую Программу (Программу исцеления) и исправить ситуацию.
В этом случае энергия, которая всегда притягивается сакральными фигурами из Пространства, так же изменит своё местоположение и притянет за собой материальную составляющую на клеточном уровне.
Когда орган примет изначальную, исконную форму, то изменится его работоспособность и здоровье в лучшую сторону. Все, что мешало, выйдет из него, подчинившись гармонии и воскресшей силе.
Геометрическая структура внутри любого органа и каждой клеточки крови, лимфы, внутри любой части тела имеет большое значение. Работая с ней можно творить чудеса.
Но, конечно же, это только часть общей работы над восстановлением физического тела. Она является составляющей того многогранного воздействия, с помощью которого вы сейчас восстанавливаете свои физические тела. Поэтому не стоит акцентировать свою работу только на ней. А подходить, как Я сказал — комплексно.
И в то же время, если вы обратите внимание на те знания, что Я даю в этой статье, то почувствуете, каким податливым становится ваше тело, когда вы осознанно работаете с его Сакральной решёткой, с помощью драгоценного сокровища — Пирамиды, которая не только усиливает вашу мысль и направляет энергию на проблемное место, но и даёт Нам возможность исправлять ситуацию.
Как это все происходит, Я уже все подробно описал в предыдущей части нашей беседы.
Но вернёмся к Тетраэдру.
Почему, сказав несколько слов о нем, я перешёл на информационную геометрическую составляющую человека и окружающего мира.
Да. Ты правильно отметила, что окружающий вас мир далёк от совершенства геометрических фигур — и это ве-ли -ко-леп-но!
Ярким представителем геометрической безукоризненности является Тетраэдр. И благодаря этой своей индивидуальности, он является цементирующей фигурой в семействе многоугольников.
Все Платоновы тела по большому счёту являются сакральными.
Их никто не видит, пока отдельные талантливые люди не отразят их на бумаге или в Пространстве.
Но на этих невидимых телах держится все видимое, материальное!Именно из этих сакральных тел строит решётку Крайон при создании новых вариантов планет или новых планет и звёзд.
Все в жизни меняется. Не меняются только Платоновы тела. Окружённые сферой, они становятся единым индивидуальным телом, содержащим в себе остов построенный по созданной Богом Программе.
И в этой решётке, какого бы размера она ни была и как бы ни выглядела, все тела являются идеальными, в отличие от энергии, которая затем обволакивает их, и в конечном счёте, при определённых условиях — материализуется.
Энергия, облепившая определённую решетку, может иметь различные внешние формы, но внутри всё равно она будет состоять изцепочек Платоновых тел.
Тетраэдр является тем гвоздиком, который соединяет, максимально приближает друг к другу любые Платоновы тела, в каких бы вибрациях они не находились.
Тетраэдр имеет очень важную особенность — каждая его грань может иметь свою вибрацию и при этом не подчинять себе, не подчинять этой вибрации другие грани. В данном случае, согласно предложенной Богом схеме, она может соединить между собой различные фигуры Сакральной геометрии.
Благодаря тетраэдрам, выстраиваются решётки любой величины и формы, как единое целое. С помощью тетраэдров более мелкие решётки присоединяются к другим, создавая более крупную цепь соединений для более крупной решётки. И так, кирпичик за кирпичиком, выстраивается вещество, равное атому или планете, или любому Космическому объекту в Мироздании.
Тетраэдр не только является связующим звеном в объектах всего видимого вам Космоса и вашего собственного внутреннего мира, но и самостоятельной фигурой, которая так же имеет место быть во Времени и Пространстве.
Тетраэдр обладает многими волшебными свойствами, как самостоятельное Сакральное тело.
Как я уже сказал, Тетраэдр — гармоничная фигура.
Это однополюсная фигура.
Уникальность её заключается в том, что она принимает энергию из Пространства всеми вершинами одинаково.
Но у каждой вершины есть своя личная сторона. И поэтому не возникает соподчинений. В том случае, когда две вершины получили одинаковый заряд, они не подчиняют себе третью вершину и сторону, а существуют каждая самостоятельно. Более того, не зависимо от состояния и качеств энергии, на поверхности стороны внутри тетраэдра всегда нейтральная энергия.
Именно, это состояние даёт ему возможность намагничивать на себя другие тела.
Тетраэдр похож на Пирамиду, но его никогда нельзя назвать Пирамидой, даже треугольной, так как это абсолютно разные фигуры, которые обладают не только принципиально разным строением, но и качеством энергии, что находятся внутри них. Это принципиально разные фигуры! Объединяет их только то, что они сильные и гармоничные, но каждая в своём амплуа.
Тетраэдр притягивает своими вершинами энергию из Пространства ещё и для того, чтобы существовать самостоятельно.
С помощью Тетраэдра можно составлять фигуры, такие как звезды — Звёздный Тетраэдр.
Звёздный Тетраэдр, состоящий только из тетраэдров смотрится, как ёжик, направивший свои иглы — вершины в Пространство. Это в буквальном смысле — звёздная фигура. Она абсолютно самостоятельна, так как живёт за счёт той энергии, что принимает из Пространства каждая её вершина.
Эта энергия очень значима, и в будущем люди будут использовать её в своей жизни!
Допустим, можно будет сделать прибор из определённого материала, который люди изобретут в достаточно скором будущем. В этом случае, можно будет ловить энергию звёзд, солнца.
Если раскрутить такой звёздный тетраэдр, то создаётся поле, которое усилит притяжение энергии должного вида из Пространства.
По специальным проводам она будет переходить в энергонакопители, а затем распространяться дальше.
Это не солнечная батарея. Её принцип работы другой, в чём-то похож по идее вылавливания энергии из Пространства, но работать он будет и днём, и ночью. А эффект захвата энергии будет больше в несколько сотен раз.
Он будет основан на знании того, что энергия из Пространства притягивается углами, а не плоскостью. Затем все это будет «сливаться» во внутренне пространство и выводиться из этой фигуры через специальный провод.
Это вечный генератор энергии. Им можно будет пользоваться не только в больших масштабах, но и на электромобилях, вертолётах, космических лайнерах. Можно ставить их и на жилые помещения и на административные здания.
При соблюдении определённых условий эксплуатации, он будет полностью безопасен. Допустим, на машине окружить его сферой с энергоотводящими путями, направленными к двигателю. Это будет бесконечный энергосборщик для различных целей людей. Вечный двигатель. Волшебный двигатель.
Тетраэдр так же может использоваться в Целительстве.
Своей самостоятельной гармонией и нейтральной энергией внутри он может давать людям успокоительный эффект. Достаточно взять его в руки и тихонько гладить по граням.
Лучше, если он будет из живого минерала. Именно это обстоятельство даст человеку возможность получить двойной целительный эффект .
– Минерал своей сакральной геометрией будет взаимодействовать с невидимой геометрией в теле человека, наполняя каждую фигуру энергией.
– В то же время, поглаживание граней и сторон тетраэдра даст эффектстягиваниячерез пальцы в нейтральную зону этой геометрической фигурытех эмоций, что будоражатв данный момент человека. Причём, не только плохих, но и хороших. Приводя его в состояние спокойствия и умиротворения.
Вот вам и ещё одно волшебное свойство Тетраэдра.
Но продолжу далее.
Тетраэдр — ангельская фигура.
Она буквально находится внутри всех ангельских сущностей, видимых и не видимых. Когда Я говорю слово видимых, я имею ввиду буквально изображение ангела, созданное человеком.
Невидимые ангелы — это Святые, Духи Предков, и просто безличностный сгусток Божественной энергии — так же содержат в себе эту фигуру.
После всего Мною сказанного, Я думаю вас это не удивляет.
Пусть не удивляет и то что Я скажу далее — в вас так же присутствует и бесчисленное множество маленьких Тетраэдров и большой, во весь рост Тетраэдр. Он не зафиксирован так фундаментально, как Икосаэдр, но информационно всё-таки есть.
К сожалению, это обстоятельство не делает из человека Ангела, но тем не менее, Я настаиваю на своём утверждении, что Тетраэдр — это ангельское существо. Оно содержит в себе энергию ангельского умиротворения равновесия и свободы.
– Что это значит?
– Дело в том, что внутри этой фигуры, изначально, не было пустоты. Этоединственное сакральное тело, которое было наполнено плотью — Божественной энергией из Центра Всего Сущего. Это является необходимым состоянием, для выполнения его миссии.
Тетраэдр выполняет миссию Миротворца.
Он должен, как Ангел, соединять несоединимое, разнополюсное, разнокачественное.
Это потрясающая по своей силе и возможностям фигура. Волшебная фигура.
К сожалению, она не может влиять на превращение человека в Ангельскую сущность, так как у последнего есть Сознание, которое является руководителем его жизни. Но тем не менее, помогает ему наполняться Божественной энергией. Кстати, в этом есть некая схожесть его с Октаэдром.
– Спасибо, Учитель! Это буквально потрясающие знания!
– Я Благословляю вас!
Светлова, Жарликов. 2016 год
http://www.soznanie.com/docs/ar64_magiya_sakralnoy_geomentii.htm
Источник: http://novayarealnost.ucoz.ru/publ/sakralnaja-geometrija/prakticheskoe-znachenie/14_piramida_i_platonovy_tela_tetraehdr/37-1-0-1511




